lecture 3

Lecture 3: 09.12.03 The first law of thermodynamics

Today:

Last Time............................................................................................................................................................... 2

Work and heat change the internal energy of a system......................................................................................... 3

The first law: conservation of energy in thermodynamic calculations................................................................................ 3

Defining work and heat............................................................................................................................................ 3

Equivalence of work and heat.................................................................................................................................... 4

Heat and work in reversible processes......................................................................................................................... 5

Path dependence vs. path independence of work, heat, and other thermodynamic functions............................................................................................................................................................... 7

Path independent variables: State functions.................................................................................................................. 7

Path dependent variables: heat and work...................................................................................................................... 7

Application example............................................................................................................................................... 9

References........................................................................................................................................................... 10

Reading: Mortimer, Ch. 3 åWork, Heat, and Energy: The First Law of Thermodynamics,π pp. 45-60

Supplementary Reading: Dill and Bromberg, Ch. 7 pp. 119-126 (further discussion of the first law, work, heat, and reversible vs. irreversible processes)

PLANNING NOTES:

Need to fill in conversion of work to heat examples

Last Time

Work and heat change the internal energy of a system

The first law: conservation of energy in thermodynamic calculations

The most general expression for the energy of a system accounts for kinetic energy (K), potential energy of position (V), and internal energy (U):

(Eqn 1)

For thermodynamic systems, we are typically interested in materials at rest (K = V = 0)- thus we focus on the internal energy.

∑ Internal energy, like kinetic and potential energy that you first encounter in physics, is conserved. Energy lost from a system is not destroyed, it is passed to its surroundings. The first law of thermodynamics is simply a statement of this conservation. The first law, mathematically, is:

Stated in simple language, the first law says that a change in internal energy is exactly accounted for by summing the contribution due to heat transferred (into or out of the system) and the work performed (on or by the system).

The first law introduces the two ways of changing the energy of a system: via heat transfer or work.

Defining work and heat

Definition of work

The meaning of mechanical work is somewhat intuitive; it is energy spent in applying a mechanical force to produce a displacement- a change in size of a system. However, work can be described in more general terms and is comprised of many other forms in addition to mechanical work.

Where dw is the rate work is performed in creating some infintessimal change in the extent of the system dx against the force F which resists that change.

You are familiar with mechanical work where F is a mechanical force and dx is a change in the length of a (one-dimensional) system, such as a spring. However, work can take on many forms. Some examples of interest for materials science & engineering include:

Examples of work in materials

Force, F	Change in systemπs extent dx in response to this force (displacement):
Pressure, P	Volume dV
Electric field, E	Charge
Chemical potential of A atoms, µ_A	Number of A atoms, NA
Surface tension, g	Surface area of system, dA

Applying pressure changes the extent of the systemπs volume V. Applying an electric field changes the extent of the systemπs charge. We will discuss some of the important forms of work in more detail a few lectures from now.

Definition of heat

We can use the first law and the definition of work given above to define heat:

Heat is thus a process, not a property of the system.

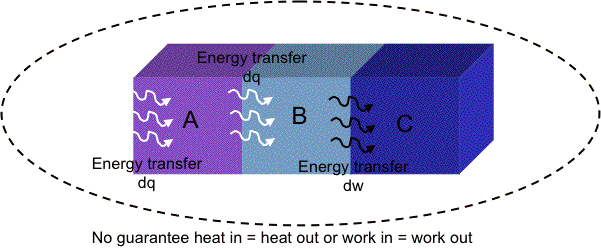
Heat and work only refer to processes of energy transfer (!!!)

Equivalence of work and heat

The first law can be thought of as a statement of energy conservation, but it is also a statement of the equivalence of work and heat. (Eqn 2) says that I could change the internal energy of a system by some amount (suppose the internal energy is increased 5 Joules, for concreteness) in two entirely different ways:

Perform 5 J of work on the system with no heat transfer at the boundaries of the system.

Transfer 5 J of heat into the system while performing no mechanical work (or any other form of work).

Combining knowledge of the type of process occurring with the first law allows one to calculate changes in internal energy directly from measurable quantities like heat and work.

Real-world example here?

Or use Joule expt. Carter p. 40

You may be intuitively comfortable with the idea that mechanical work can convert to heat through processes such as friction. Others following Joule confirmed that all forms of work- not just mechanical work- can be converted to heat.

Example of electrical work -> heat?

Heat and work in reversible processes

P-V work in reversible processes

Pressure on a system performs work at a rate that is well defined only if the work is done extremely slowly, such that the system is in equilibrium at all times and none of the mechanical work being done is converted to heat.

This is referred to as a quasi-static process- it is reversible.
In such a process, the rate at which work is performed is:

The total work for a quasi-static process is readily calculated by integrating:

(Eqn 7)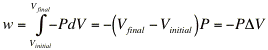

We can only integrate -PdV when the process is reversible!

Heat transfer is linked to an entropy change in reversible processes

Our first real encounter with entropy comes in examining heat transfer in a reversible process, which provides one definition of entropy:

This equation provides some initial insight into the meaning of entropy, for reversible processes:

The reversible process definition of entropy provides a means to measure entropy changes during reversible processes. It is the heat change in a system divided by the systemπs temperature.
The definition also allows us to show the link between entropy and internal energy. Combining the first law with (Eqn 11):

(Eqn 9) for a reversible process

In a reversible process where no mechanical work is performed, dU = TdS.

Path dependence vs. path independence of work, heat, and other thermodynamic functions

Path independent variables: State functions

We have introduced several thermodynamic functions:

Internal energy U = U(S,V,N)
Entropy S = S(U,V,N)
Pressure P = P(V,N,T)

Weπve just seen how the internal energy depends on S and V for the case of reversible processes. We will show in a few lectures how U also depends on N.

We have also introduced heat and work:

Heat q heat transfer rate; dq
Work w rate of work done on system: dw

The thermodynamic functions above are distinct from work and heat: U,S, and P are examples of state functions, while q and w are not state functions

State functions are models for materials

If I know 3 variables, the fourth is determined by the state function

State functions are path independent:

A state function can be integrated to calculate changes in the value of the function:

Path-dependent functions like heat and work, on the other hand, can only be integrated in reversible processes.

Path dependent variables: heat and work

Work and heat are not state functions; they are path dependent- what does this mean?
In most physical situations, we are concerned with a quantity of heat or work transferred into or out of a material, which causes a change from one state of the material to another. Path dependence implies that the amount of work or heat needed to make the change depends on how the process was performed, not just what state the material started in and ended in.

A simple example: path dependence of P-V work

If mechanical work is performed on a material by placing it under pressure extremely slowly- such that none of the work is converted to heat (e.g. due to friction) and the system is in equilibrium at each moment, then the work performed is given by:

(Eqn 12)

Suppose I have a block of material that I put under various conditions, varying the pressure the material is under and itπs volume. I do this to change from a state A (P₁, V₁) to state B (P₂, V₂) by two different paths, as illustrated below:

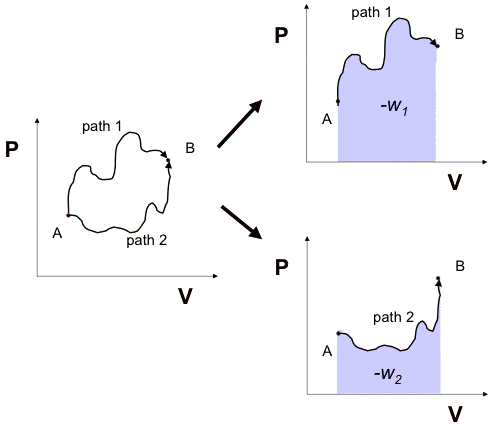
How might these nonlinear paths be obtained in a real experiment?

Since I performed this work extremely slowly (without waste of any of the work as heat), we can calculate the total work for each path by integrating (Eqn 12):

(Eqn 13)

We can clearly see from the graphical representation that the work done along path 1 will be significantly different from that along path 2: the total work is path dependent.

Summary of characteristics of path dependence: