13.021 Marine Hydrodynamics, Fall 2003

Lecture 2

13.021 - Marine Hydrodynamics
Lecture 2

Chapter 1 - Basic Equations

1.1 - Description of a Flow.

Flows are often defined either by an Eulerian description or a Lagrangian description.

Eulerian description: This is a field description that is often easy to apply. The velocities of the flow are given at fixed points in space as time varies. Imagine a case where both the measuring device and the frame of reference are fixed.
The velocity, pressure, density, ...can be mathematically represented as follows:
$\vec{v}(\vec{x},t), p(\vec{x},t), \rho(\vec{x},t), \ldots$
Lagrangian description: This description is easier to understand but harder to apply. Here the quantities of the flow are given for a particular moving particle at varying times. The velocity, pressure, density, ...can be mathematically represented as follows:
$\vec{v}_{p}(t), p_{p}(t), \rho_{p}(t), \ldots$

Useful terms for flow description

Streamline: A line everywhere tangent to the fluid velocity $\vec{v}$ at a given time. In an Eulerian description, it would be a `snapshot' of the flow (See tutorial ).
Streakline: Instantaneous locus of all particles that pass a given point. In an Eulerian description, it would be a `snapshot' of certain particles (See tutorial ).
Pathline: The trajectory of a given particle P in time. The photograph analogy would be a long time exposure of a given particle (See tutorial ).

Some Eulerian Quantities of Interest

Scalars: have magnitude only.
Pressure: $p\left( \vec{x},t \right)$ ; Density: $\rho \left( \vec{x},t \right)$
Vectors: have magnitude and direction

$\displaystyle \vec{v}$ $\displaystyle = u\hat{i}+v\hat{j}+w\hat{k}$

$\displaystyle =u_{1}\hat{x_{1}}+u_{2}\hat{x_{2}}+u_{3}\hat{x_{3}}$

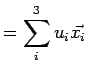$\displaystyle =\sum_{i}^{3} u_{i}\vec{x_{i}}$

$\displaystyle = u_{i} \vec{x_{i}}$ Einstein Notation

Einstein Notation: Repeated indices are summed by implication over all values of the index i. In this example, the summation is over i =1, 2, 3.

Note that if the equation looks like this: $\left( u_{i} \right) \left( \vec{x}_{i} \right)$ , the indices are not summed.

For a fluid flow to be continuous, we require that the velocity $\vec{v}(\vec{x},t)$ be a finite and continuous function of $\vec{x}$ and t. i.e. $\nabla \cdot \vec{v}$ and $\frac{\partial \vec{v} }{ \partial t}$ are finite but not necessarily continuous. Since $\nabla \cdot \vec{v}$ and $\frac{\partial \vec{v} }{ \partial t}$ < $\infty$ , there is no infinite acceleration, which is physically consistent.

Consequences of Continuous Flow

Material volume remains material. No segment of fluid can be joined or broken apart.
Material surface remains material. The interface between two material volumes always exists.
Material line remains material. The interface of two material surfaces always exists.

$\begin{figure} \begin{center} \epsfig{file=lfig21.eps,height=1.5in,clip=} \end{center} \end{figure}$
Material neighbors remain neighbors. To prove this mathematically, we must prove that, given two particles, the distance between them at time t is small, and the distance between them at time t + $\delta$ t is still small.

Given: Two particles with initial position $\vec{x}$ and $\vec{x}+\delta\vec{x}$ , initial time t and the fluid velocity v.

Proof:

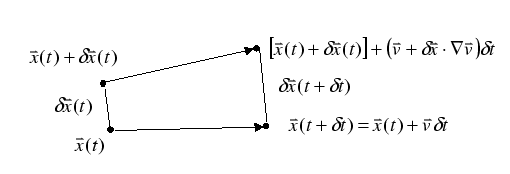
$\begin{figure} \begin{center} \epsfig{file=lfig22.eps,height=1.5in,clip=} \end{center} \end{figure}$

Where $\vec{v}\delta t$ is the distance travelled by the particle. The difference in position between the two particles is:

$\displaystyle \left[\vec{x}(t)+\delta\vec{x}(t)\right]+\left(\vec{v}+\delta\vec... ...\vec{v}\right)\delta t-\vec{x}(t)-\vec{v}\delta t = \delta\vec{x}(t+\delta t)$

(1)

$\displaystyle \Rightarrow \delta\vec{x}(t+\delta t) = \delta\vec{x}(t)+\delta\vec{x}(t)\cdot\nabla\vec{v}\delta t \propto \delta\vec{x}(t)$

Therefore $\delta\vec{x}(t+\delta t) \propto \delta \vec{x}(t)$ since $\nabla \vec{v}$ is finite due to the continuous flow assumption. Therefore if $\delta \vec{x}(t) \rightarrow 0$ , then $\delta \vec{x}(t+\delta t) \rightarrow 0$ . In fact, for any time period T,

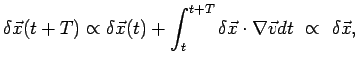$\displaystyle \delta \vec{x}(t+T) \propto \delta \vec{x}(t)+\int_{t}^{t+T}\delta\vec{x}\cdot\nabla \vec{v}dt \propto \delta\vec{x},$

and $\delta \vec{x}(t+T) \rightarrow 0$ as $\delta \vec{x}(t) \rightarrow 0$ , therefore the particles will never be an infinite distance apart. Thus the flow is continuous and two particles that are neighbors will always be neighbors.

Material/Substantial Derivative: D/Dt

A material derivative is the time derivative - rate of change - of a property `following a fluid particle P'. The material derivative is a Lagrangian concept but we will work in an Eulerian reference frame.

Consider an Eulerian quantity $f(\vec{x},t)$ . Taking the Lagrangian time derivative of an Eulerian quantity gives the material derivative. The Lagrangian time derivative is:

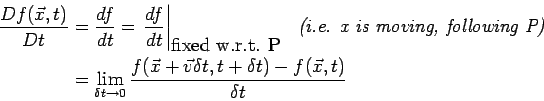$\begin{displaymath}\begin{split} \frac{Df(\vec{x},t)}{Dt} & =\frac{df}{dt} =\le... ...vec{v}\delta t,t+\delta t)-f(\vec{x},t)}{\delta t} \end{split}\end{displaymath}$

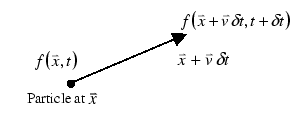
$\begin{figure} \begin{center} \epsfig{file=lfig23.eps,height=1in,clip=} \end{center} \end{figure}$

P is moving at an Eulerian velocity $\vec{v} = \frac{\delta\vec{x}}{\delta t}$ . Performing a 3D Taylor series on f gives:

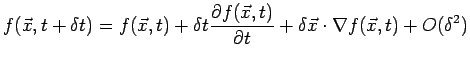$\displaystyle f( \vec{x},t+\delta t) = f(\vec{x},t)+\delta t\frac{\partial f(\vec{x},t)}{\partial t}+\delta \vec{x}\cdot\nabla f(\vec{x},t)+O(\delta^{2})$ (higher order terms)

Therefore the substantial derivative is:

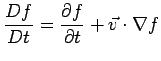$\displaystyle \frac{Df}{Dt} =\frac{\partial f}{\partial t} +\vec{v}\cdot\nabla f$

With the generalized notation:

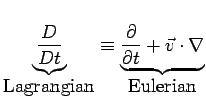$\displaystyle \underset{\mbox{Lagrangian}}{\underbrace{\frac{D}{Dt} }} \equiv ... ...mbox{Eulerian}}{\underbrace{\frac{\partial }{\partial t} +\vec{v}\cdot\nabla }}$

Example: Lagrangian acceleration of a particle. Consider the Eulerian velocity $\vec{v}(\vec{x},t)$ . Then the Lagrangian acceleration is:

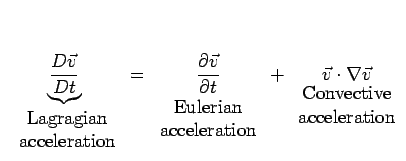$\displaystyle \underset{\mbox{ \begin{tabular}{c} Lagragian acceleration \... ...lar}{c} Convective acceleration \end{tabular}}}{\vec{v}\cdot\nabla\vec{v}}$

Difference between Lagrangian time derivative and Eulerian time derivative

Example: Consider an Eulerian quantity, temperature, in a room at points A and B where the temperature is different at each point.

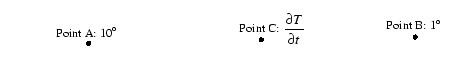
$\begin{figure} \begin{center} \epsfig{file=lfig24.eps,width=4in,clip=} \end{center} \end{figure}$

At point C, the temperature rate of change is $\frac{\partial T}{\partial t}$ which is an Eulerian time derivative.

Example: Consider the same example as above: an Eulerian quantity, temperature, in a room at points A and B where the temperature varies with time.

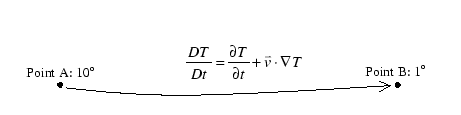
$\begin{figure} \begin{center} \epsfig{file=lfig25.eps,width=4in,clip=} \end{center} \end{figure}$

Following a particle from point A to B, the Lagrangian time derivative would need to include the temperature gradient as time and position changed: $\frac{DT}{Dt} =\frac{\partial T}{\partial t} +\vec{v}\cdot\nabla T$

Concept of a Steady Flow

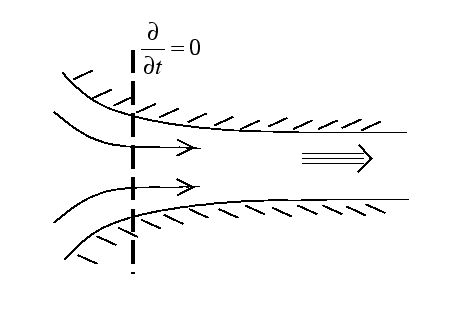
Assume a steady flow where the flow is observed from a fixed position. This is like watching from a river bank, i.e. $\frac{\partial }{\partial t} =0$ . Be careful not to confuse this with $\frac{D}{Dt}$ which is more like following a twig in the water. Note that $\frac{D}{Dt} =0$ does not mean steady since the flow could speed up at some points and slow down at others.

$\begin{figure} \begin{center} \epsfig{file=lfig26.eps,width=4in,clip=} \end{center} \end{figure}$

Karl P Burr 2003-08-31

$\displaystyle \vec{v}$	$\displaystyle = u\hat{i}+v\hat{j}+w\hat{k}$
	$\displaystyle =u_{1}\hat{x_{1}}+u_{2}\hat{x_{2}}+u_{3}\hat{x_{3}}$
	$\displaystyle =\sum_{i}^{3} u_{i}\vec{x_{i}}$
	$\displaystyle = u_{i} \vec{x_{i}}$ Einstein Notation