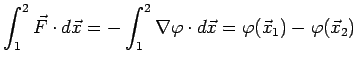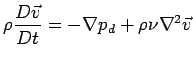13.021 Marine Hydrodynamics, Fall 2003
Lecture 4
Copyright © 2003 MIT - Department of Ocean
Engineering,
All rights reserved.
13.021 - Marine Hydrodynamics
Lecture 4
Governing Equations so far:
|
Knowns |
Number of Equations |
Number of Unknowns |
|
|
Continuity(conservation of
mass) |
1 |
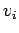 |
3 |
|
|
Euler (conservation of
momentum) |
3 |
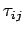 |
6
3 of 9 eliminated by symmetry |
|
|
|
4 |
|
9 |
Therefore, some constitutive relationships are needed to relate
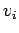 to
to 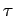
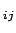 .
.
- Consider a fluid at rest (
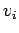
 0). Then according to
Pascal's Law:
0). Then according to
Pascal's Law:
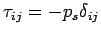 (Pascal's
Law) (Pascal's
Law)![$\displaystyle \hspace{1.0in} \underset{ }{\tau} =\left[
\begin{array}{ccc}
-p_{s} & 0 & 0 \
0 & -p_{s} & 0 \
0 & 0 & -p_{s}
\end{array}
\right]$](img9.gif) |
|
where 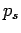 is the hydrostatic pressure and
is the hydrostatic pressure and
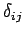 is the
Kroenecker delta function, equal to
is the
Kroenecker delta function, equal to 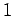 if
if 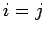 and 0 if
and 0 if 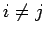 .
.
- Consider a fluid in motion. The fluid stress is defined as:
where 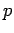 is the thermodynamic pressure and
is the thermodynamic pressure and
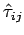 is
the dynamic stress, which is related to the velocities
empirically.
is
the dynamic stress, which is related to the velocities
empirically.
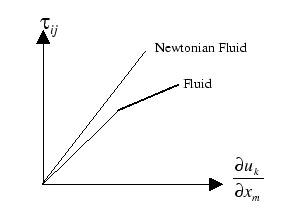
Experiments with a wide class of fluids, "Newtonian"
fluids, obtain that:
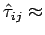 linear function of the linear function of the
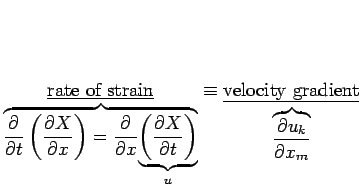 |
|
i.e. 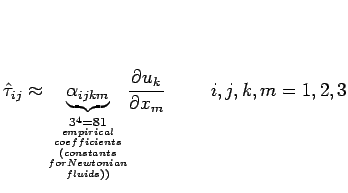 |
|
Note that the shear stress is proportional to the rate of strain.
For isotropic fluids, this reduces to:
where the fluid properties are:
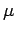 - (coefficient of) dynamic viscosity.
- (coefficient of) dynamic viscosity.
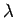 - bulk elasticity, `second' coefficient of viscosity
- bulk elasticity, `second' coefficient of viscosity
For incompressible flow,
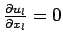 . Therefore, for an incompressible, isotropic, Newtonian fluid
the viscous stress
. Therefore, for an incompressible, isotropic, Newtonian fluid
the viscous stress
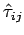 is given as
is given as
|
Equations |
Number of Equations |
Unknowns |
Number of Unknowns |
|
Euler |
3 |
|
3 |
|
continuity |
1 |
|
1 |
|
constitutive (Newtonian) |
6 (symmetry) |
|
6 |
|
|
10 |
|
10 |
|
|
|
Substitute the equation for the stress tensor
for a Newtonian fluid into Euler's equation:
where
and
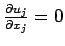 due to continuity.
Finally,
due to continuity.
Finally,
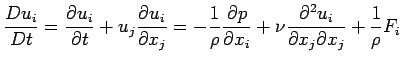 |
Tensor form |
|
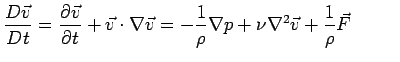 |
Vector form |
|
where
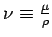 denoted as the
Kinematic viscosity [
denoted as the
Kinematic viscosity [ 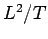 ].
].
- Navier-Stokes equations for incompressible, Newtonian fluids
|
|
Number of Equations |
|
Number of Unknowns |
|
continuity |
1 |
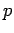 |
1 |
|
Navier-Stokes |
3 (symmetry) |
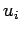 |
3 |
|
|
4 |
|
4 |
- Kinematic Boundary Conditions: Specifies kinematics (position, velocity,
...) On a solid boundary, velocity of the fluid = velocity of
the body. i.e. velocity continuity.
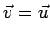 "no-slip" boundary condition "no-slip" boundary condition |
|
where 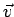 is the fluid velocity at the body and
is the fluid velocity at the body and 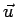 is
the body surface velocity
is
the body surface velocity
-
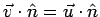 no flux - continuous
flow
no flux - continuous
flow
-
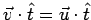 no slip -
finite shear stress
no slip -
finite shear stress
figure
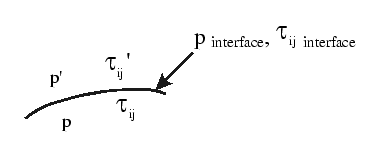
- Dynamic Boundary Conditions: Specifies dynamics ( pressure, sheer stress, ...
)
Stress continuity:
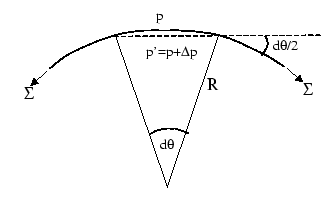
The most common example of interfacial stress is surface tension.
figure
- Conservative force:
where 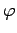 is the force potential.
is the force potential.
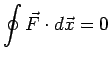 or or 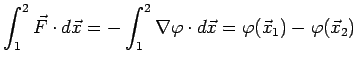 |
|
- A special case of a conservative force is gravity.
with Gravitational potential:
where 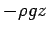 is the hydrostatic pressure
is the hydrostatic pressure
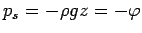 .
.
Navier-Stokes equation:
but
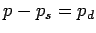 and p
and p
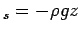 , where
, where
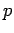 is the total pressure and
is the total pressure and 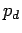 is the dynamic pressure.
Therefore,
is the dynamic pressure.
Therefore,
- Presence of gravity body force is equivalent to replacing
total pressure
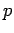 by dynamic pressure
by dynamic pressure 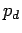 in the
Navier-Stokes(N-S) equation.
in the
Navier-Stokes(N-S) equation.
- Solve the N-S equation with
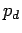 , then calculate
, then calculate
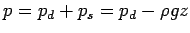 .
.
Karl P Burr
2003-08-27
![]() to
to ![]()
![]() .
.
![$\displaystyle \hspace{1.0in} \underset{ }{\tau} =\left[
\begin{array}{ccc}
-p_{s} & 0 & 0 \
0 & -p_{s} & 0 \
0 & 0 & -p_{s}
\end{array}
\right]$](img9.gif)
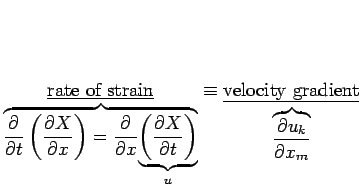
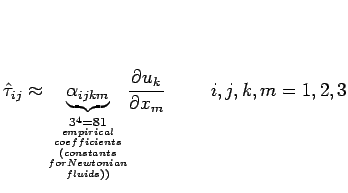

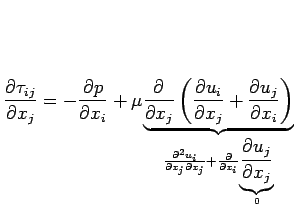
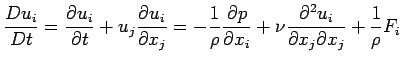
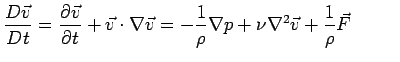
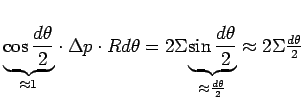
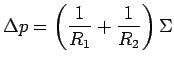
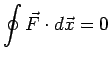 or
or