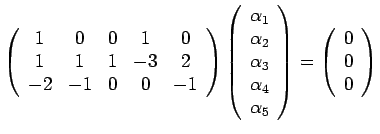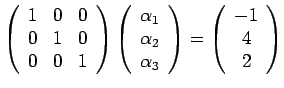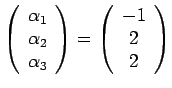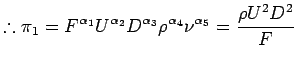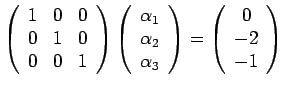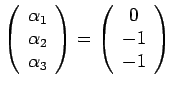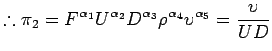13.021 Marine Hydrodynamics, Fall 2003
Lecture 5
Copyright © 2003 MIT - Department of Ocean
Engineering,
All rights reserved.
13.021 - Marine Hydrodynamics
Lecture 5
Similitude: Similarity of behavior of different systems.
Real world
 ``model''
``model''
(prototype) (physical experiment, mathematical,
computer, ...)
| |
Similarity Parameters (SP's) |
| Geometric Similitude |
length ratios |
| Kinematic Similitude |
Displacement ratios, velocity ratios |
| Dynamic (Internal
Constitution) |
Force ratios, stress ratios, pressure ratios |
|
|
|
| Internal Constitution
Similitude |
|
| Boundary Condition
Similitude |
|
|
|
|
|
|
 |
Reduce number of
variables
 derive dimensionally homogeneous
relationships.
derive dimensionally homogeneous
relationships.
- Specify (all) the (say N) relevant variables
(dependent or independent):
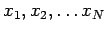
e.g. time, force, fluid density, distance...
We want to relate the 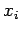 's to each other
's to each other
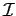 (
(
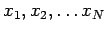 ) = 0
) = 0
- Identify (all) the (say P) relevant basic physical units (``dimensions'')
e.g. M,L,T (P = 3) [temperature, charge, ...].
- Let
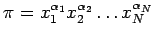 be a dimensionless quantity formed from the
be a dimensionless quantity formed from the
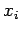 's. Suppose
's. Suppose
where the 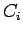 are dimensionless constants. For example, if
are dimensionless constants. For example, if
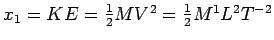 (kinetic energy), we have that
(kinetic energy), we have that
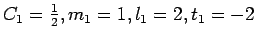 . Then
. Then
For  to be dimensionless, we require
to be dimensionless, we require
 |
(1) |
Since (1) is homogeneous, it always has a trivial
solution,
 (i.e. (i.e.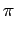 is constant) is constant) |
|
There are 2 possibilities:
- (1) has no nontrivial solution (only solution is
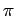 =
constant, i.e. independent of
=
constant, i.e. independent of 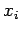 's), which implies that the N
variable
's), which implies that the N
variable
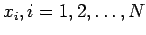 are
Dimensionally Independent (DI), i.e. they are
"unrelated" and "irrelevant" to the problem.
are
Dimensionally Independent (DI), i.e. they are
"unrelated" and "irrelevant" to the problem.
- (1) has
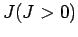 nontrivial solutions,
nontrivial solutions, 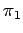 ,
,
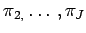 . In general,
. In general, 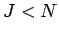 , in fact,
, in fact, 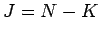 where
where 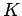 is
the rank or "dimension" of the system of equations
(1).
is
the rank or "dimension" of the system of equations
(1).
Instead of relating the N
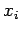 's by
's by
 (
(
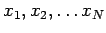 )
= 0, relate the
)
= 0, relate the 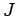
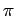 's by
's by
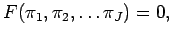 where where 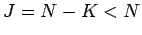 |
|
For similitude, we require
If 2 problems have all the same 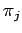 's, they have similitude
(in the
's, they have similitude
(in the 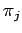 senses), so
senses), so 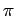 's serve as similarity
parameters.
's serve as similarity
parameters.
Note:
In general, we want the set (not unique) of independent
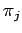 's, for e.g.,
's, for e.g., 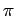
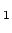 ,
, 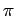
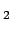 ,
, 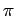
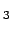 or
or
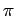
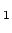 ,
, 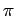
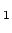
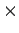
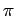
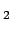 ,
, 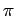
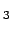 , but
not
, but
not 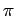
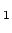 ,
, 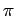
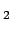 ,
, 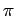
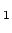
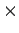
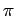
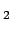 .
.
Application of Buckingham
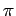 Theory.
Theory.
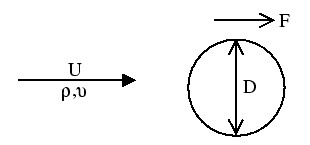
Figure 1:
Force on a smooth circular cylinder
in steady incompressible fluid (no gravity)
 |
|
N = 5 |
|
|
|
|
|
|
|
|
|
P = 3 |
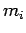 |
1 |
0 |
0 |
1 |
0 |
|
|
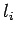 |
1 |
1 |
1 |
-3 |
2 |
|
|
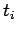 |
-2 |
-1 |
0 |
0 |
-1 |
For 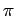 to be non-dimensional, the set of equations
to be non-dimensional, the set of equations
has to be satisfied. The system of equations above after we
substitute the values for the 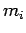 's,
's, 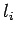 's and
's and 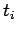 's
assume the form:
's
assume the form:
The rank of this system is 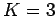 , so we have
, so we have 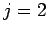 nontrivial
solutions. Two families of solutions for
nontrivial
solutions. Two families of solutions for
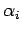 for each
fixed pair of (
for each
fixed pair of (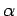
 ,
,
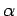
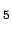 ), exists a unique solution for (
), exists a unique solution for (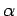
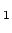 ,
, 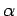
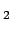 ,
,
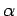
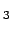 ). We consider the pairs (
). We consider the pairs (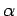
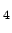 = 1,
= 1,
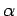
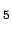 = 0) and (
= 0) and (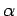
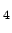 = 0,
= 0,
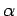
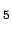 = 1), all other cases are linear
combinations of these two.
= 1), all other cases are linear
combinations of these two.
- Pair
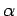
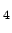 = 1 and
= 1 and 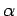
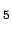 = 0.
= 0.
which has solution
Conventionally,
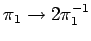 and
and
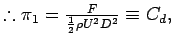 which is the Drag coefficient.
which is the Drag coefficient.
- Pair
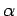
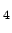 = 0 and
= 0 and 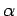
 =
1.
=
1.
which has solution
Conventionally,
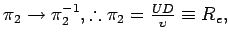 which is the Reynolds
number.
which is the Reynolds
number.
Therefore,
Karl P Burr
2003-08-27