| velocity | U |
|
| length | L |
|
| time | T |
|
| pressure | p |
|
13.021 - Marine Hydrodynamics, Fall 2003
Lecture 6
Copyright © 2003 MIT - Department of Ocean
Engineering,
All rights reserved.
Non-dimensionalize and normalize basic equations by
scaling:
Identify characteristic scales for the problem
All ()* quantities are dimensionless and normalized (i.e. O(1)), e.g.
![]() . Apply to governing equations: (also internal constitution, boundary conditions)
. Apply to governing equations: (also internal constitution, boundary conditions)
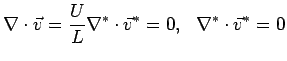
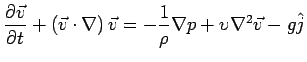
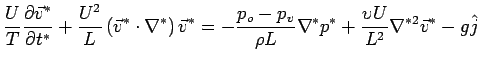
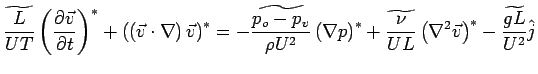
 measure the relative importance of each term (as compared to the convective inertia term):
measure the relative importance of each term (as compared to the convective inertia term):
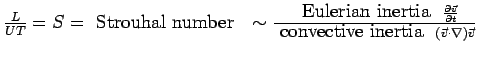


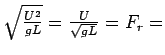 Froude number
Froude number

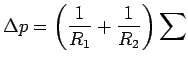 |
||
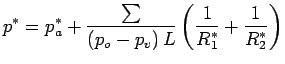 |
||
where 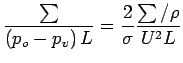 |

note:
![]() usually
usually
Alternatively, using physical arguments: forces acting on a fluid particle
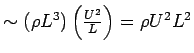
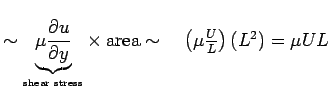
For similar streamlines, particles must be acted on by forces whose resultant is in the same direction at geosimilar points. Therefore, forces must be in the same ratios:
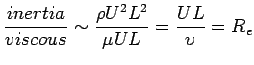
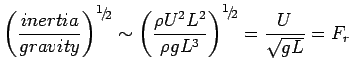
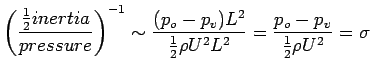
For example, hydrofoil traveling close to the fluid surface.
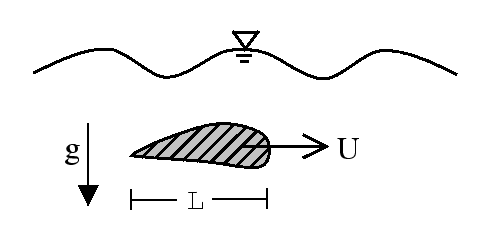
Parameters:
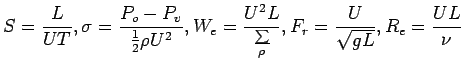 |
Force coefficient on the foil:
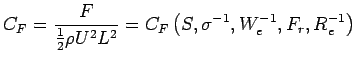 |
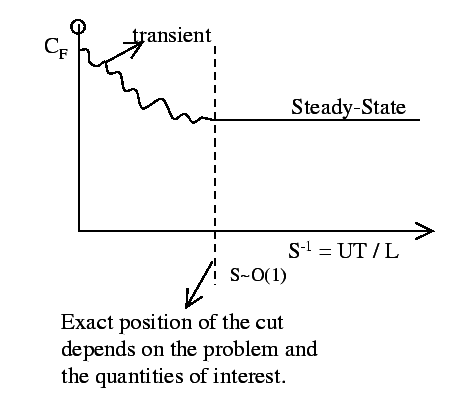
For ![]() , assume steady-state:
, assume steady-state:
![]()
For ![]() , unsteady effect is dominant.
For example:
, unsteady effect is dominant.
For example:
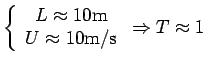 seconds gives seconds gives |
So, for steady-state problem:
| P |
vapor pressure | ||||
|
|
State of fluid changes from liquid to gas
|
||||
| Mechanism: |
|
||||
| Consequence: | (1) Unsteady
(2) Unstable |
||||
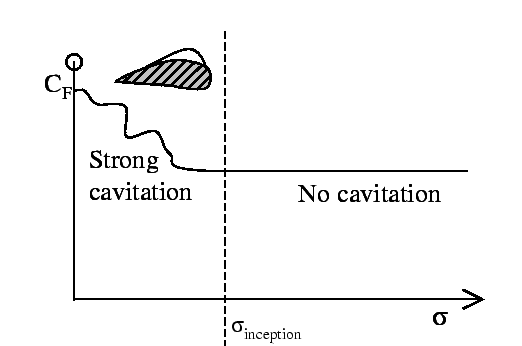
For
![]() , there is cavitation, and for
, there is cavitation, and for
![]() , there is no cavitation. For example:
, there is no cavitation. For example:
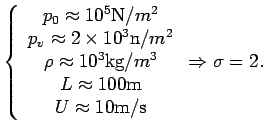 To have cavitation we need large To have cavitation we need large |
Note: ![]() is the pressure at which the water boils.
is the pressure at which the water boils.
For steady non-cavitation flow (
![]() )
)
For steady, non-cavitation, non-surface tension effect,
For problems without dynamic boundary conditions (i.e.
if free surface is absent) or if the free-surface is far away or
not displaced, gravity effects are irrelevant and ![]() is not
important
is not
important
![]()
e.g.
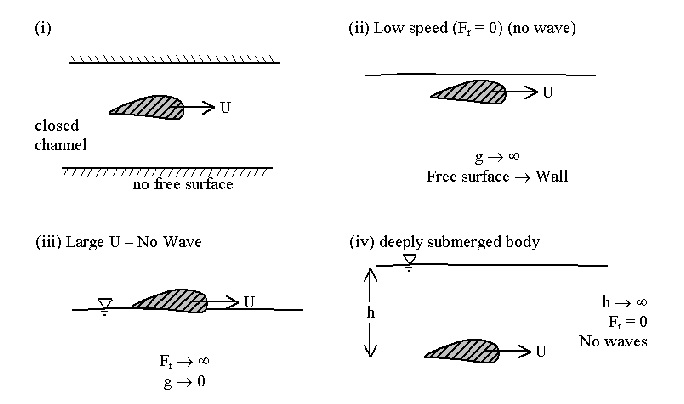
In general
![]() Froude's Hypothesis
Froude's Hypothesis
Dynamic similarity requires:
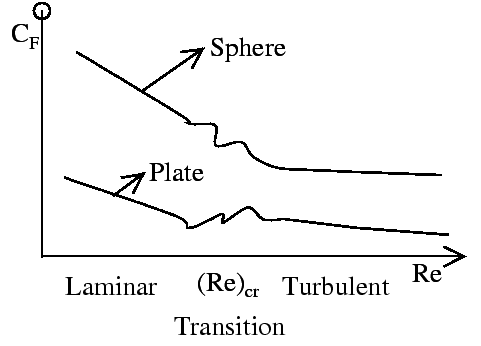
| Stokes flow (creeping flow) | ||
| Laminar flow | ||
| Turbulent flow | ||
| Ideal flow |
For example:
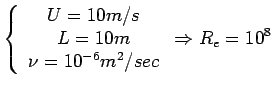 or or
|
For steady, no ![]() , no
, no ![]() , no gravity effect and ideal fluid:
, no gravity effect and ideal fluid:
![]() D'Alembert's Paradox: No drag force on moving body.
D'Alembert's Paradox: No drag force on moving body.