Tutorial - Ilustration of Kelvin's Theorem - Relation between Circulation and Vorticity.
The purpose of this tutorial is to illustrate:
- The action of the velocity field over a closed material contour by using the vector field manipulation application. The user can type the desired equations for the velocity field, then chose the Draw Contour option from the drop down box, then input a closed contour by mouse clicking the contour edges, change the value of time in the Input t text box, and click the Draw button to see the new shape and position of the material contour.
- To illustrate Kelvin's theorem through simple velocity fields,
- To illustrate the connection between vorticity and circulation through simple velocity fields.
We first consider a simple velocity field which satisfies Laplace's equation and has zero vorticity. The velocity field is
and
This velocity field satisfies Euler's equation if the pressure gradient is given by the equations:
and
where 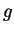 is the gravity acceleration constant. From the two equations above, the pressure is given by the equation
is the gravity acceleration constant. From the two equations above, the pressure is given by the equation
where 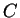 is an integration constant defined by the boundary conditions. Then, this velocity field satisfies the hypothesis in Kelvin's theorem, so the circulation on any closed material contour should be constant, and in this special case the value of the circulation is zero. One way to check this affirmation is just to compute the circulation on a closed material contour, and the reader can use the vector field manipulation application. Another way is to take a look on the vorticity of this velocity field. The vorticity for this case is given by the equation
is an integration constant defined by the boundary conditions. Then, this velocity field satisfies the hypothesis in Kelvin's theorem, so the circulation on any closed material contour should be constant, and in this special case the value of the circulation is zero. One way to check this affirmation is just to compute the circulation on a closed material contour, and the reader can use the vector field manipulation application. Another way is to take a look on the vorticity of this velocity field. The vorticity for this case is given by the equation
The circulation around any material contour is related to the vorticity flux across a surface limited by the integration contour according to Stoke's theorem. Therefore, for this particular velocity field the circulation on any closed material contour is zero. The reader can use the vector field manipulation application to check this by doing the following exercise:
- 1.
- The velocity field above is the default vector field in the vector field manipulation application. The user should chose the option Draw Contour from the drop down box in the application panel, and then click the button Draw from the application panel.
- 2.
- By mouse clicking in the display area the user can input a contour made of straight lines. For example, the user may input a square contour.
- 3.
- The user can know click the circulation button for the application to evaluate the circulation on the inputed closed contour. It should be zero.
- 4.
- Next, the user should change the value of time in the Input t text box. After that, the user should click the Draw button, and the new shape and position of the contour is displayed. To have a better representation of the convected contour, the user should input a large value for the number of points per side of the contour to advance in time in the text box named # of points per side to advance in time. Since the velocity field satisfies Laplace's equation, the area enclosed by the contour remains the same.
- 5.
- Now, the user should click the circulation button to see the new value of the circulation around the new contour. It should be zero.
Next, we consider a velocity field which satisfies Laplace's equation but has a constant vorticity. It is given by the equations:
and
This velocity field satisfies Euler's equation if the pressure gradient is given by the equations:
and
where 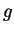 is the gravity acceleration constant. From the two equations above, the pressure
is the gravity acceleration constant. From the two equations above, the pressure 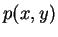 is
is
and this velocity field satisfies the hypothesis in Kelvin's theorem, so the circulation on any closed material contour should be constant, and in this special case the value of the circulation is equal to the value of the area enclosed by the contour. One way to check this affirmation is just to compute the circulation on a closed material contour, and the reader can use the vector field manipulation application. Another way is to take a look on the vorticity of this velocity field. The vorticity in this case is
Since the vorticity for this velocity field is constant, for a closed contour which encircles an area of value 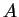 ,
the circulation
,
the circulation 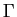 in this case is just the vorticity times the area, then
in this case is just the vorticity times the area, then
The reader can use the vector field manipulation application to check this by doing the following exercise:
- 1.
- The velocity field above can be typed in the appropriate text boxes of the vector field manipulation application. The user should chose the option Draw Contour from the drop down box in the application panel, and then click the button Draw from the application panel.
- 2.
- By mouse clicking in the display area the user can input a contour made of straight lines. It should be a contour which encloses an area with value easily evaluated. A good choice is a square contour.
- 3.
- The user can know click the circulation button for the application to evaluate the circulation on the inputed closed contour. It should be equal to the value of the area encircled by the contour.
- 4.
- Next, the user should change the value of time in the Input t text box. After that, the user should click the Draw button, and the new shape and position of the contour is displayed. To have a better representation of the convected contour, the user should input a large value for the number of points per side of the contour to advance in time in the text box named # of points per side to advance in time. Since the velocity field satisfies Laplace's equation, the area enclosed by the contour remains the same.
- 5.
- Now, the user should click the circulation button to see the new value of the circulation around the new contour. It should be the same as before.
Next, we consider a velocity field which satisfies Laplace's equation and which has variable vorticity. It is given by
and
If this velocity field satisfies Euler's equation, the pressure gradient should satisfies the equations:
and
There is no pressure function 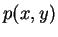 which has the gradient given by the two equations above. Therefore, this velocity field does not satisfy Euler's equation, and so it does not satisfy Kelvin's theorem, and the circulation on a closed material contour may change with time. This can be confirmed by evaluating the vorticity of this velocity field. The vorticity in this case is given by
which has the gradient given by the two equations above. Therefore, this velocity field does not satisfy Euler's equation, and so it does not satisfy Kelvin's theorem, and the circulation on a closed material contour may change with time. This can be confirmed by evaluating the vorticity of this velocity field. The vorticity in this case is given by
and the circulation on a closed contour in this case is not the vorticity times the value of the area defined by the closed contour. In terms of the vorticity the circulation is given by the integral of the vorticity over the area defined by the closed contour. What we want to illustrate in this case is that, as the closed material contour is being convected with the fluid, the circulation on it changes. To see this, the reader can use the vector field manipulation application and do the following exercise:
- 1.
- The velocity field above can be typed in the appropriate text boxes of the vector field manipulation application. The user should also change the default values in the text boxes Input x0, Input xN, Input y0 and Input yN. The user should type:
- Text box Input x0:
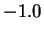 ,
,
- Text box Input xN:
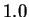 ,
,
- Text box Input y0:
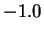 ,
,
- Text box Input yN:
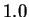 .
.
After that, the user should chose the option Draw Contour from the drop down box in the application panel, and then click the button Draw from the application panel.
- 2.
- By mouse clicking in the display area the user can input a contour made of straight lines. It should be a contour with simple geometry, like a square for example. It should be inside the area
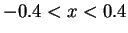 and
and
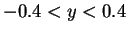 .
.
- 3.
- The user can know click the circulation button for the application to evaluate the circulation on the inputed closed contour. Keep the circulation value given by the application.
- 4.
- Next, the user should change the value of time in the Input t text box from
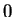 to
to 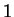 .
After that, the user should click the Draw button, and the new shape and position of the contour is displayed. To have a better representation of the convected contour, the user should input a large value for the number of points per side of the contour to advance in time in the text box named # of points per side to advance in time. Since the velocity field satisfies Laplace's equation, the area enclosed by the contour remains the same.
.
After that, the user should click the Draw button, and the new shape and position of the contour is displayed. To have a better representation of the convected contour, the user should input a large value for the number of points per side of the contour to advance in time in the text box named # of points per side to advance in time. Since the velocity field satisfies Laplace's equation, the area enclosed by the contour remains the same.
- 5.
- Now, the user should click the circulation button to see the new value of the circulation around the new contour. It has a different value and it should have decrease, since most of the area inside the contour is transported by the fluid to the first quadrant and by the fact that the vorticity is negative for positive values of the
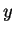 variable.
variable.
- 6.
- The reader can repeat the process from the third item down, but with a different value of time. Be careful for the convected contour do not fall outside the display area. Try a value of time
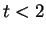 .
.
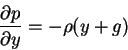
![]() is the gravity acceleration constant. From the two equations above, the pressure is given by the equation
is the gravity acceleration constant. From the two equations above, the pressure is given by the equation
![]() is an integration constant defined by the boundary conditions. Then, this velocity field satisfies the hypothesis in Kelvin's theorem, so the circulation on any closed material contour should be constant, and in this special case the value of the circulation is zero. One way to check this affirmation is just to compute the circulation on a closed material contour, and the reader can use the vector field manipulation application. Another way is to take a look on the vorticity of this velocity field. The vorticity for this case is given by the equation
is an integration constant defined by the boundary conditions. Then, this velocity field satisfies the hypothesis in Kelvin's theorem, so the circulation on any closed material contour should be constant, and in this special case the value of the circulation is zero. One way to check this affirmation is just to compute the circulation on a closed material contour, and the reader can use the vector field manipulation application. Another way is to take a look on the vorticity of this velocity field. The vorticity for this case is given by the equation
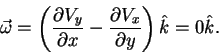
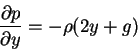
![]() is the gravity acceleration constant. From the two equations above, the pressure
is the gravity acceleration constant. From the two equations above, the pressure ![]() is
is
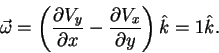
![]() ,
the circulation
,
the circulation ![]() in this case is just the vorticity times the area, then
in this case is just the vorticity times the area, then
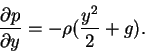
![]() which has the gradient given by the two equations above. Therefore, this velocity field does not satisfy Euler's equation, and so it does not satisfy Kelvin's theorem, and the circulation on a closed material contour may change with time. This can be confirmed by evaluating the vorticity of this velocity field. The vorticity in this case is given by
which has the gradient given by the two equations above. Therefore, this velocity field does not satisfy Euler's equation, and so it does not satisfy Kelvin's theorem, and the circulation on a closed material contour may change with time. This can be confirmed by evaluating the vorticity of this velocity field. The vorticity in this case is given by