Tutorial - Examples of Velocity Fields -Translation, Pure strain, Angular Deformation and Pure Rotation.

The purpose of this tutorial is to give examples of velocity fields which affects material contours in a specific way. We consider velocity fields which just translate a material contour, or just only strains the material contour (no volume change), or just makes an angular deformation of the material contour, or just rotates the material contours.

Translation.

Any velocity field of the form

$\begin{displaymath}V_{x} = U \end{displaymath}$

and

$\begin{displaymath}V_{y} = V, \end{displaymath}$

just translates any given material element of the fluid. To illustrate this, the user can use the vector field manipulation application. Type the vector field above in the appropriate text boxes, but with . Then input in the display area, by mouse clicking, a square contour. Then change the value of time in the text box Input t, and then click the Draw button. As a result the contour is translated by the vector field. Repeat it as many times as you want.

Pure Strain.

A velocity field $\vec{v}$ that only produces pure strain should satisfy

$\begin{displaymath}\nabla\cdot\vec{v} = 0 \end{displaymath}$

(no volume dilatation) and also no rotation is allowed. This implies that velocity field components have to satisfy

$\begin{displaymath}\frac{\partial V_{y}}{\partial x} = 0 \end{displaymath}$

and

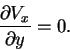
$\begin{displaymath}\frac{\partial V_{x}}{\partial y} = 0. \end{displaymath}$

As a result, the velocity field is of the form

$\begin{displaymath}V_{x} = Cx+C_{1} \end{displaymath}$

and

$\begin{displaymath}V_{y} = -Cy+C_{2}, \end{displaymath}$

where $C, C_{1}$ and $C_{2}$ are constants. As an example of a vector field that only causes pure strain to a material element of the flow, consider the case where the constants $C, C_{1}$ and $C_{2}$ assume the values $C = 1, C_{1} = 0$ and $C_{2} = 0$ . Non-zero values of the constants $C_{1}$ and $C_{2}$ would have given a translation component to the velocity field. To illustrate the effect of this velocity field to a material contour, the user can use the vector field manipulation application. Type in the text box Input $V_{x}$ and type in the text box Input $V_{y}$ . Then input in the display area, by mouse clicking, a square contour. Then change the value of time in the text box Input t, and then click the Draw button. As a result the contour suffers pure strain by the vector field. Repeat it as many times as you want.

Angular Deformation.

Now we consider the case of angular deformation. There is no volume change, so the velocity field has zero divergence ( $\nabla\cdot\vec{v} = 0$ ). There is also no rotation of any material element of the flow, so the vorticity is zero, which implies that the vector field has to satisfy

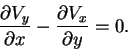
$\begin{displaymath}\frac{\partial V_{y}}{\partial x}-\frac{\partial V_{x}}{\partial y} = 0. \end{displaymath}$

As a result, the vector field has the form

$\begin{displaymath}V_{x} = Cy+C_{1}x \end{displaymath}$

and

$\begin{displaymath}V_{y} = Cx-C_{1}y, \end{displaymath}$

where and $C_{1}$ are constants. The part of the vector field multiplied by the constant $C_{1}$ gives only pure strain. Therefore, a vector field which has angular deformation as its main effect has the form

$\begin{displaymath}V_{x} = Cy \end{displaymath}$

and

$\begin{displaymath}V_{y} = Cx. \end{displaymath}$

As an example of a vector field that only causes angular deformation to a material element of the flow, consider the case where the constants assumes the values . To illustrate the effect of this velocity field to a material contour, the user can use the vector field manipulation application. Type in the text box Input $V_{x}$ and type in the text box Input $V_{y}$ . Then input in the display area, by mouse clicking, a square contour. Then change the value of time in the text box Input t, and then click the Draw button. As a result the contour suffers angular deformation by the vector field. Repeat it as many times as you want. Notice that strain is also observed.

Pure Rotation.

Now we consider velocity fields which cause pure rotation only. There is no volume change of material elements, which implies that the velocity field has zero divergence ( $\nabla\cdot\vec{v} = 0$ ). We can specify the value of the angular velocity as $\Omega$ . Then the velocity field has to satisfy the equations

$\begin{displaymath}\frac{\partial V_{y}}{\partial x} = \Omega \end{displaymath}$

and

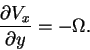
$\begin{displaymath}\frac{\partial V_{x}}{\partial y} = -\Omega. \end{displaymath}$

Therefore, the general form of the velocity field under such restrictions are given by the equations

$\begin{displaymath}V_{x} = -\Omega y+Cx \end{displaymath}$

and

$\begin{displaymath}V_{y} = \Omega x -Cy, \end{displaymath}$

where is a constant. The part of the vector field multiplied by the constant is responsible only for strain of a material element of the flow, given no contribution to rotation. Then, velocity field which has rotation as its main effect is of the form

$\begin{displaymath}V_{x} = -\Omega y \end{displaymath}$

and

$\begin{displaymath}V_{y} = \Omega x. \end{displaymath}$

As an example of a vector field that only causes rotation to a material element of the flow, we can set $\Omega =1$ in the equations above. To illustrate the effect of this velocity field to a material contour, the user can use the vector field manipulation application. Type in the text box Input $V_{x}$ and type in the text box Input $V_{y}$ . Then input in the display area, by mouse clicking, a square contour. Then change the value of time in the text box Input t, and then click the Draw button. As a result the contour suffers rotation by the vector field. Repeat it as many times as you want.