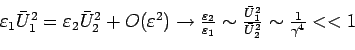A vortex tube (filament) is a bundle of vortex lines.
13.021 - Marine Hydrodynamics, Fall 2003
Lecture 8
Copyright © 2003 MIT - Department of Ocean
Engineering,
All rights reserved.
A vortex line is a line everywhere tangent to
![]()
A vortex tube (filament) is a bundle
of vortex lines.
Example (figures) of natural vortex tubes are tornados (see figures: 1, 2, 3, 4, 5 and 6), watersprouts (similar as a tornado, but occurs over bodies of water. See figures 1, 2, 3, 4, 5 and 6) and dust devils (see figure 1 and figure 2 for a martian dust devil). Vortex tubes generated at the tip of aircraft wings (see figures 1, 2, 3, 4 and 5), at the tip of propellers (see figures 1 and 2) and at other parts of an aircraft wing and fuselage (see figures 1 and 2) are examples of man made vortex tubes and lines.
Some Properties:
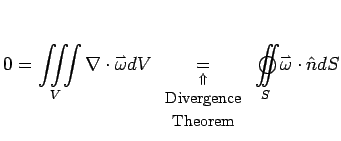 |
No net flux of vorticity through a closed surface. For example, a vortex tube:
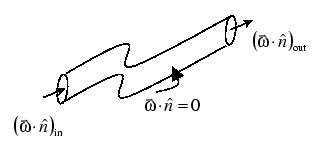
Vorticity cannot stop anywhere in the fluid. It either closes on itself or traverses the fluid beginning or ending on a boundary. A vortex line/tube has no beginning and no end anywhere in the fluid, only on a boundary.
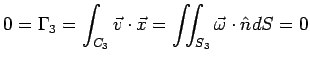
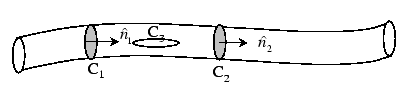
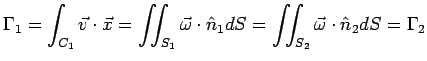
Therefore, circulation is the same in all circuits embracing the same vortex tube. For the special case of a vortex tube with "small" area:
An application of the equation above is displayed in the figure below:

Consider a material patch ![]() on a vortex tube at
time
on a vortex tube at
time ![]() .
.
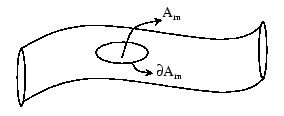
By definition,
Then,
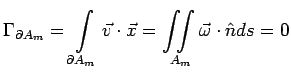
At time t + ![]() t,
t, ![]() moves, and for
an ideal fluid under the influence of conservative body forces,
Kelvin's theorem states that:
moves, and for
an ideal fluid under the influence of conservative body forces,
Kelvin's theorem states that:
Consider a small vortex filament of length L and radius R.
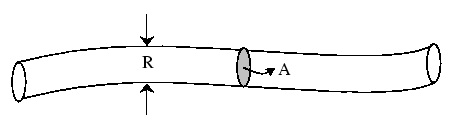
![]() is tangent to tube.
is tangent to tube.
 constant (in time), constant (in time), |
But tube is material with volume = AL = ![]() R
R![]() L =
constant in time (continuity)
L =
constant in time (continuity)
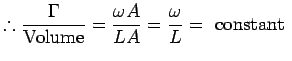 |
As a vortex stretches, ![]() increases, and since the volume is
constant (from continuity),
increases, and since the volume is
constant (from continuity), ![]() and
and ![]() decrease, and due to the
conservation of the angular momentum,
decrease, and due to the
conservation of the angular momentum, ![]() increases. In
other words,
increases. In
other words,
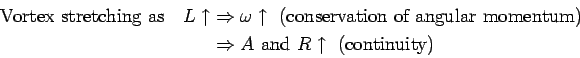 |
| Viscous flow: Navier-Stokes' Equation | ||
| Ideal flow: Bernoulli Equation |
(BI): Bernoulli eq. for steady (Rotational in general) Ideal flow
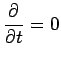
Steady, inviscid Euler equation: (momentum equation)
From Vector Calculus:
Then we write
From equations (1) and (4), we have that
Then,
![]() (5) gives
(5) gives
and which implies that
The equation (7) above states that the gradient of the quantity
is ortogonal to the velocity vector ![]() . In other words, the quantity
. In other words, the quantity ![]() does not vary in the direction of the velocity vector. Since the velocity vector is tangent to the streamlines, que quantity
does not vary in the direction of the velocity vector. Since the velocity vector is tangent to the streamlines, que quantity ![]() is constant along the streamlines so
is constant along the streamlines so
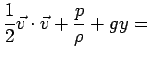 constant constant |
along the streamline. Since the flow is steady, we can write
which implies that the ![]() is constant along a material element of the flow. In general we write
is constant along a material element of the flow. In general we write
where ![]() is a tag for a particular streamline.
is a tag for a particular streamline.
Assumptions: Ideal fluid, Steady (Rotational or not) flow.
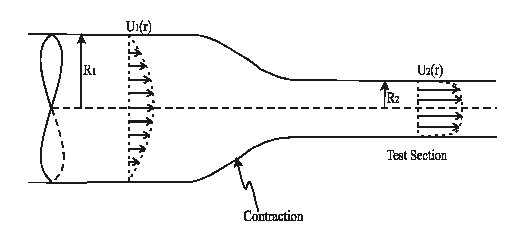
Contraction Ratio:
![]() (
(
![]() for wind ;
for wind ;
![]() for water).
for water).
Let
![]() and
and
![]() be average velocity
at section 1 and 2 respectively.
be average velocity
at section 1 and 2 respectively.
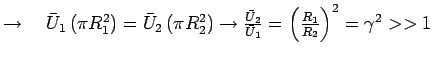
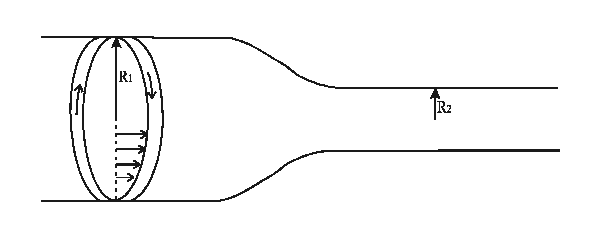
Since
![]() vortex ring.
vortex ring.
i.e.
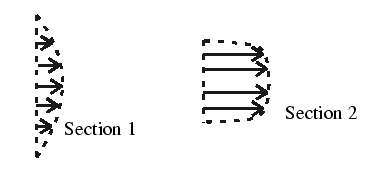
where
![]() and
and
![]() measure
the relative velocity fluctuations. Apply the Bernoulli equation
along a reference average streamline
measure
the relative velocity fluctuations. Apply the Bernoulli equation
along a reference average streamline
Apply Bernoulli Equation to a particular streamline: