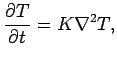
We illustrate the behaviour of the diffusion equation
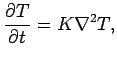
where ![]() is, for example, a temperature distribution.
is, for example, a temperature distribution. ![]() in this case is the heat diffusivity. We consider the one-dimensional case, so
in this case is the heat diffusivity. We consider the one-dimensional case, so
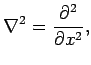
and
![]() . We consider a Gaussian tenperature distribution as initial condition, which is given by the equation
. We consider a Gaussian tenperature distribution as initial condition, which is given by the equation
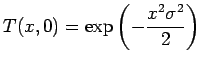
This initial value problem can be solved by using the Fourier transform. Details of the solution are omitted and left as an exercise. The temperature distribution at an instant ![]() is given by the equation
is given by the equation
We illustrate this solution by using a java applet. Just click on the equation above. The parameter ![]() controls the shape of the initial temperature distribution. The parameter
controls the shape of the initial temperature distribution. The parameter ![]() controls how fast the temperature difuses. They can assume very small values, so we use the log scale in this parameter slider bar.
controls how fast the temperature difuses. They can assume very small values, so we use the log scale in this parameter slider bar.