First, we obtain the ![]() and
and ![]() components of the velocity vector.
components of the velocity vector.
 |
 |
Second, we make the change of variables
We substitute the expressions for ![]() and
and ![]() in terms of
in terms of ![]() and
and ![]() in the equations for
in the equations for ![]() and
and ![]() .
Then, we set
.
Then, we set ![]() ,
and we define
,
and we define
![]() and
and ![]() .
Now we write
.
Now we write
 |
 |
Third, evaluate the radial velocity ![]() at the circles surface. The radial velocity
at the circles surface. The radial velocity ![]() can be written in terms of the velocities
can be written in terms of the velocities ![]() and
and ![]() according to the equation
according to the equation
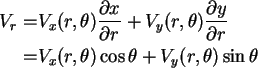
With this equation and the equations for ![]() and
and ![]() at the surface of the circle, we have
at the surface of the circle, we have
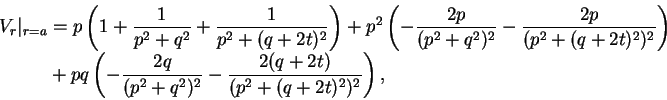 |