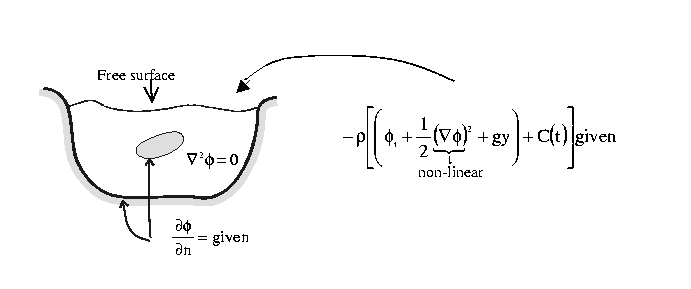The pressure in the air side of the interface is the atmospheric pressure ![]() ,
and it can be assumed constant and independent of the water surface position. At the fluid side of the interface, the pressure is given by the Bernoulli equation, and chosing the integration constant
,
and it can be assumed constant and independent of the water surface position. At the fluid side of the interface, the pressure is given by the Bernoulli equation, and chosing the integration constant ![]() suitably, the dynamic boundary condition to be satisfied at the water surface is
suitably, the dynamic boundary condition to be satisfied at the water surface is
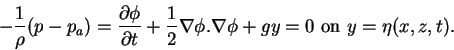 |
Example: Body submerged in a body of water.