If
![]() are harmonic functions (they satisfy Laplace's equation, i.e.
are harmonic functions (they satisfy Laplace's equation, i.e.
![]() ), then
), then
![]() ,
where
,
where
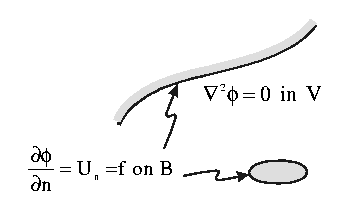
![]() are constants, are also harmonic, and is the solution for the boundary value problem provided the boundary conditions (kinematic boundary condition) are satisfied, i.e.
are constants, are also harmonic, and is the solution for the boundary value problem provided the boundary conditions (kinematic boundary condition) are satisfied, i.e.
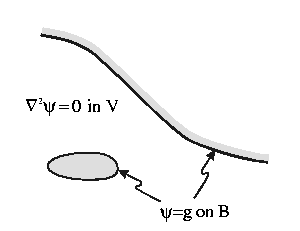
The same is true for the stream function ![]() .
K.B.C.s
specify the value of
.
K.B.C.s
specify the value of ![]() on the boundaries.
on the boundaries.