


Next: Solution: Equations for the
Up: 3.7 - Simple Potential
Previous: Uniform Stream
Potential function for 2D source of strength m at r = 0:
It satisfies
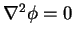 (check Laplace's equation in polar coordinate in the keyword search utility), except at
(check Laplace's equation in polar coordinate in the keyword search utility), except at
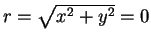 (so must exclude r = 0 from flow)
(so must exclude r = 0 from flow)
- 1.
- Question: Derive the equations for the velocity field for the 2D source.
- (a)
- Hint: expression for the gradient in polar coordinates (use the keyword utility: coordinate system - velocity vector)
- 2.
- Question: Evaluate the outward volume flux.
- (a)
- Hint: Consider a contour which contains the 2D source.
- (b)
- Hint: Use Gauss theorem to deform the contour into a small circle of radius
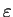 around the source.
around the source.
- (c)
- Hint: Evaluate the flux in the direction normal to the circle (radial velocity) and integrate along the circle.
If
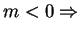 sink. Source with strength
sink. Source with strength 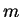 located at
located at
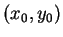 :
:
3D source - Spherical coordinates
A spherically symmetric solution:
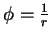 (verify
(verify
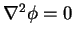 except at
except at 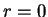 )
)
Define 3D source of strength 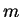 located at
located at 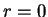 :
:
- 1.
- Question: Evaluate the net outward volume flux.
Keyword Search



Next: Solution: Equations for the
Up: 3.7 - Simple Potential
Previous: Uniform Stream
![]() (check Laplace's equation in polar coordinate in the keyword search utility), except at
(check Laplace's equation in polar coordinate in the keyword search utility), except at
![]() (so must exclude r = 0 from flow)
(so must exclude r = 0 from flow)
![]() sink. Source with strength
sink. Source with strength ![]() located at
located at
![]() :
:
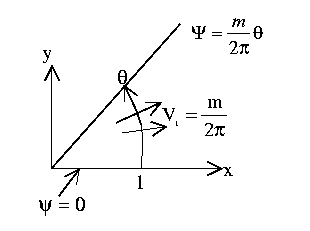
![]() (verify
(verify
![]() except at
except at ![]() )
)
![]() located at
located at ![]() :
: