


Next: Solution: radial velocity ,
Up: 3.7 - Simple Potential
Previous: Solution: Net outward flux
Another particular solution:
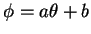 (verify
(verify
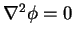 except at
except at 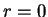 )
)
Potential function for a point vortex of circulation
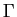 at
at 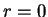 :
:
Stream function:
- 1.
- Question: Evaluate the radial velocity
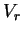 ,
the tangential velocity
,
the tangential velocity
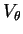 and the vorticity
and the vorticity
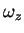 .
.
- (a)
- Hint: velocity vector in polar coordinates (use the keyword utility: coordinate system - velocity vector).
- (b)
- Hint: write the vorticity
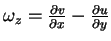 in polar coordinates.
in polar coordinates.
- 2.
- Question: Evaluate the circulation
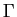 along an arbitrary closed contour containing the 2D vortex.
along an arbitrary closed contour containing the 2D vortex.
- (a)
- Hint: deform the closed contour to a circle containing the 2D vortex at the origin.
- (b)
- Hint: evaluate the velocity tangent to the circle.
- (c)
- Hint: integrate the tangent velocity along the circle.
Keyword Search



Next: Solution: radial velocity ,
Up: 3.7 - Simple Potential
Previous: Solution: Net outward flux
![]() (verify
(verify
![]() except at
except at ![]() )
)
![]() at
at ![]() :
: