


Next: Solution: stagnation points for
Up: 3.7 - Simple Potential
Previous: Solution: cross-sectional area of
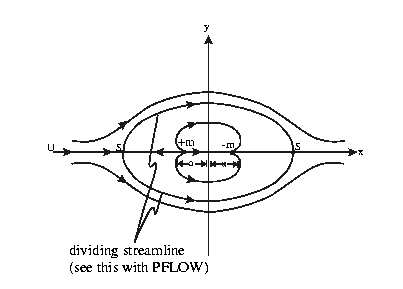
To have a closed body, a necessary condition is to have
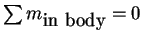
2D Rankine ovoid:
Stagnation Points for 2D Rankine ovoid
3D Rankine ovoid:
- 1.
- Question: Find the stagnation points for the 3D Rankine ovoid.
- (a)
- Hint: derive the velocity vector
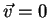 .
.
- (b)
- Hint: solve
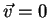 for
for 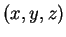 .
.
- 2.
- Question: Find the radius
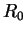 of the body.
of the body.
- (a)
- Hint: mass flux at the half body equals
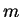 .
.
Keyword Search

![]()
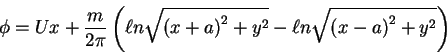
![\begin{displaymath}\phi = Ux - \frac{m}{4\pi }\left[ {\frac{1}{\sqrt {\left( {x ...
...rac{1}{\sqrt {\left( {x - a} \right)^2 + y^2 + z^2} }}
\right]
\end{displaymath}](img131.gif)