We can impose a kinematic boundary condition on the water surface. We assume that the water surface is at
![]() (
(![]() is the time parameterization), and the kinematic boundary condition in this case will be
is the time parameterization), and the kinematic boundary condition in this case will be
where
![]() .
With this expression for
.
With this expression for ![]() ,
the condition above reduces to
,
the condition above reduces to
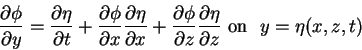 |