Up: No Title
Previous: No Title
D'Alembert: ideal, irrotational, unbounded, steady.
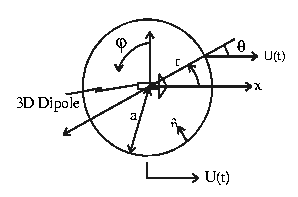
Example 1: Force on a sphere accelerating (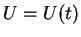 ,
unsteady) in an unbounded fluid at rest. (at infinity)
,
unsteady) in an unbounded fluid at rest. (at infinity)
K.B.C on sphere:
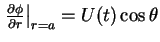
Solution: Simply a 3D dipole (no stream)
Check:
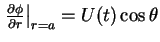
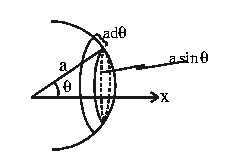
Hydrodynamic force:
On r = a:
Finally,
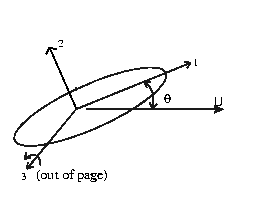
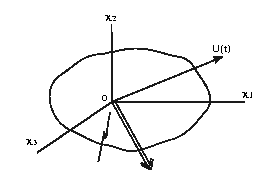
General 6 degrees of freedom motions
Added mass matrix (tensor)
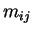 :
associated with force on body in
:
associated with force on body in 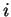 direction
due to unit acceleration in
direction
due to unit acceleration in 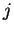 direction. For example, for a
sphere:
direction. For example, for a
sphere:
Some added masses of simple 2D geometries
- circle
figure
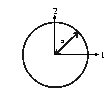
- ellipse
figure
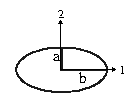
- plate
figure
- square
figure
A reasonable estimate for added mass od a 2D body is to
use the displaced mass (
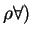 of an ``equivalent
cylinder'' of the same lateral dimension or one that ``rounds
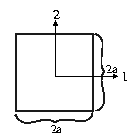
off'' the body. For example, we consider a aquare:
of an ``equivalent
cylinder'' of the same lateral dimension or one that ``rounds
off'' the body. For example, we consider a aquare:
- 1.
- inscribed circle:
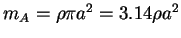 .
.
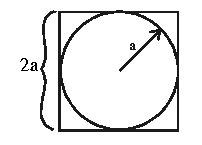
- 2.
- circumscribed circle:
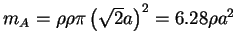 .
.
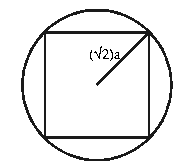
Arithmetic mean of 1) + 2)
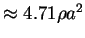 .
.
General 6 degrees of freedom forces and moments on a rigid body
moving
in an unbounded fluid ( at rest at infinity)
Note:
 fixed in the body.
fixed in the body.
Then (JNN §4.13)
Einstein's 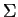 notation applies.
notation applies.
Note:
- 1.
- if
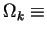 0 ,
0 ,
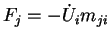 (as
expected by definition of
(as
expected by definition of 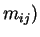 .
Also if
.
Also if
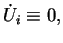 then
then 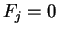 for any
for any 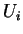 ,
no force in steady translation.
,
no force in steady translation.
- 2.
-
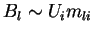 ``added momentum'' due to rotation of
axes, 2)
``added momentum'' due to rotation of
axes, 2) 
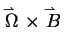 where
where
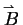 is linear momentum. (momentum from 1 coordinate into new
is linear momentum. (momentum from 1 coordinate into new
 direction)
direction)
- 3.
- If
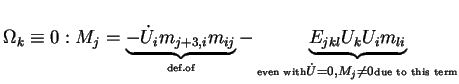 .
.
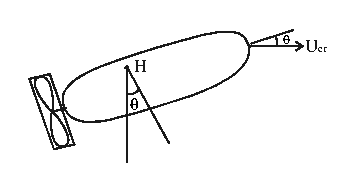
Moment on a body due to pure steady
translation - ``Munk'' moment.
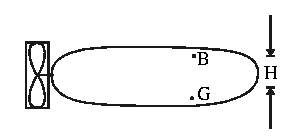
Example of Munk Moment - a 2D submarine in steady
translation
Consider steady motion:
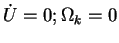 .
Then
.
Then
For a 2D body,
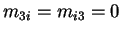 ,
also
,
also
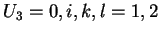 .
This implies that:
.
This implies that:
Therefore, 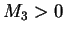 for
for
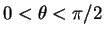 ("Bow
up"). Therefore, a submarine under forward motion is unstable in
pitch (yaw) (e.g., a small bow-up tends to grow with time), and
control surfaces are needed:
("Bow
up"). Therefore, a submarine under forward motion is unstable in
pitch (yaw) (e.g., a small bow-up tends to grow with time), and
control surfaces are needed:
Usually
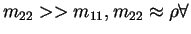 .
For small
.
For small
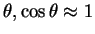 .
So,
.
So,
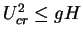 or
or
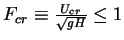 .
Otherwise, control fins are required.
.
Otherwise, control fins are required.


Up: No Title
Previous: No Title

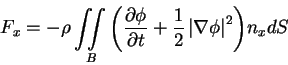
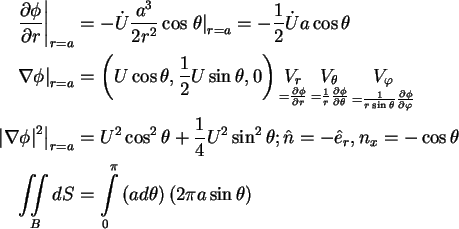
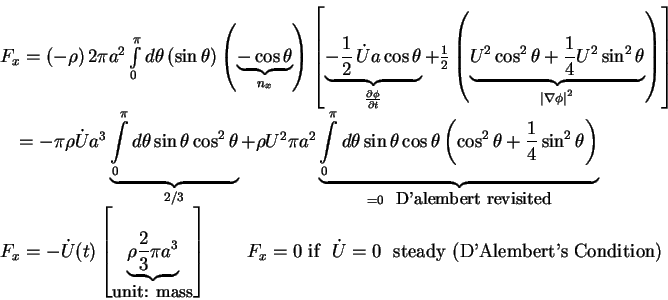
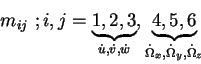
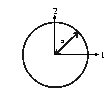




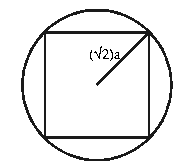
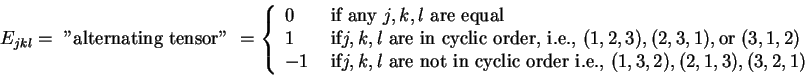
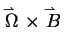 where
where
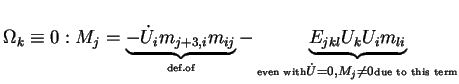 .
.