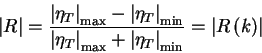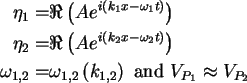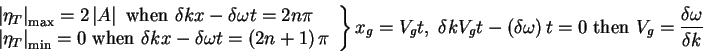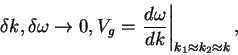Next: Wave Energy - Energy
Up: Free-surface waves: linear superposition,
Previous: Free-surface waves: linear superposition,
- 1.
- oblique plane waves:
figure
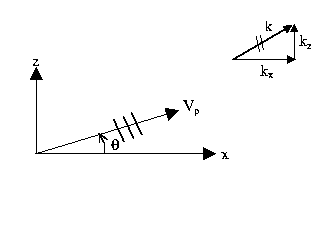
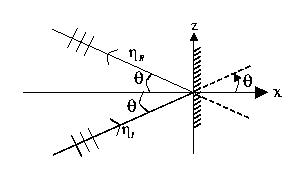
Consider wave propagation at an angle 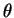 to the
x-axis
to the
x-axis
- 2.
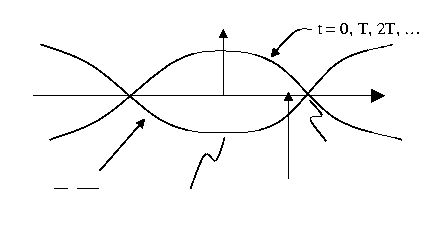
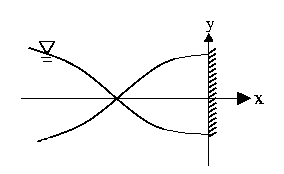
- Standing Waves:
Therefore,
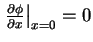 .
To obtain an standing wave, it is necessary
to have perfect reflection at the wall at
.
To obtain an standing wave, it is necessary
to have perfect reflection at the wall at 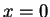 .
figure
.
figure
- 3.
- Oblique Standing Waves.
Note: same A, R = 1.
and
Check:
- 4.
- Partial Reflection.
figure
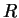 :
Complex reflection coefficient
:
Complex reflection coefficient
![\begin{align}\mbox{R } = & \mbox{ }\left\vert \mbox{R} \right\vert e^{ - i\delta...
...{R} \right\vert\cos \left( {2kx + \delta }
\right)} \right] \notag
\end{align}](img20.gif)
figure
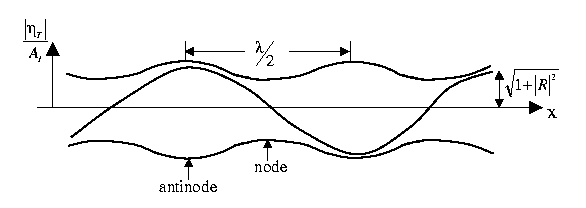
At node,
At antinode,
- 5.
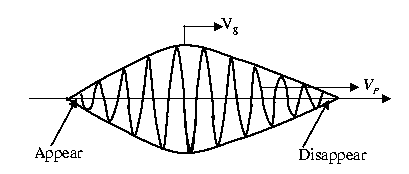
- Wave Group 2 waves, same amplitude A and
direction, but
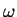 and
and  very close to each other.
very close to each other.
In the limit,
and since
Keyword Search



Next: Wave Energy - Energy
Up: Free-surface waves: linear superposition,
Previous: Free-surface waves: linear superposition,
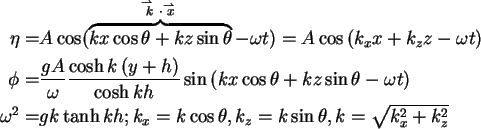

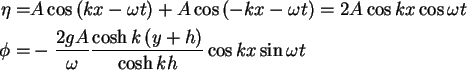
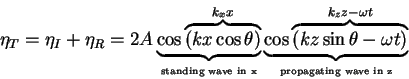

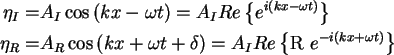
![\begin{align}\mbox{R } = & \mbox{ }\left\vert \mbox{R} \right\vert e^{ - i\delta...
...{R} \right\vert\cos \left( {2kx + \delta }
\right)} \right] \notag
\end{align}](img20.gif)

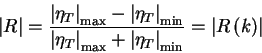


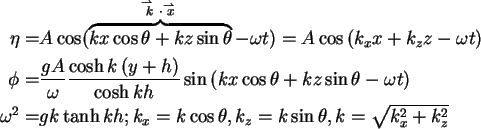

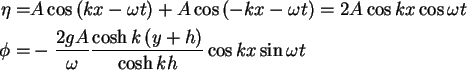



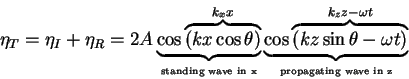

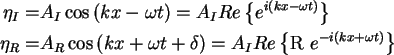
![\begin{align}\mbox{R } = & \mbox{ }\left\vert \mbox{R} \right\vert e^{ - i\delta...
...{R} \right\vert\cos \left( {2kx + \delta }
\right)} \right] \notag
\end{align}](img20.gif)