Thermal Fluctuations
Finite Size Scaling at Criticality
![]() Correlation
lengths diverge at a critical point:
Correlation
lengths diverge at a critical point:
Finite-size contribution of long-wavelength fluctuations at criticality:
![]()
M.E. Fisher and P.-G. de Gennes, C. R. Acad. Sci. Ser. B 287, 207 (1978)
Can be attractive or repulsive depending on boundary conditions (like or unlike)
The parameter c=Θ(0) is a universal constant, related (in 2d) to the central charge in conformal field theory.
H.W.J. Blote, J.L. Cardy, and M.P. Nightingale, Phys. Rev. Lett. 56, 742 (1986)
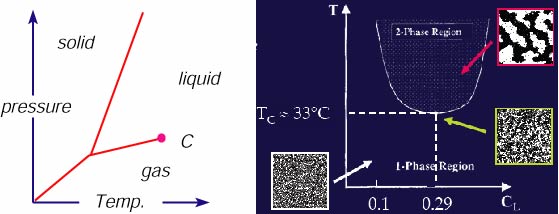
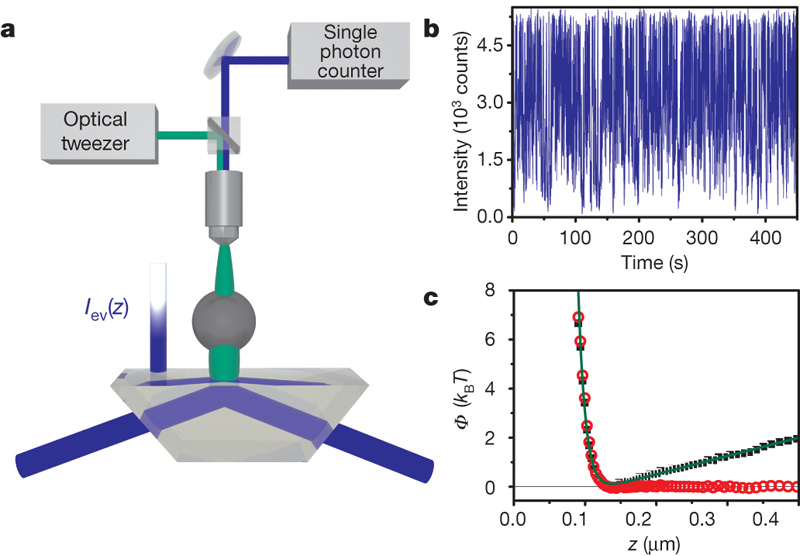
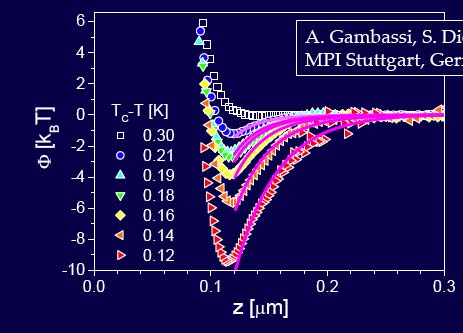
Colloidal particles in a critical binary mixture
![]() "Direct
measurement of critical Casimir forces,"
"Direct
measurement of critical Casimir forces,"
Hertlein, Helden, Gambassi, Dietrich & Bechinger, Nature 451, 172 (2008)
Superfluid Helium
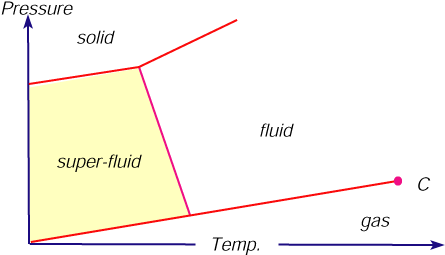
![]() The superfluid
phase of helium supports phonons ("mass-less" Goldstone
modes)
The superfluid
phase of helium supports phonons ("mass-less" Goldstone
modes)
![]() .
.
The interaction resulting from (thermal) fluctuations of these modes is:
![]()
H. Li . Kardar, Phys. Rev. Lett. 67, 3275 (1991); Phys. Rev. A 46, 6490 (1992)
Wetting by a Superfluid Film
![]() Garcia and Chan monitored
thickness of a wetting film of helium near the superfluid transition.
Garcia and Chan monitored
thickness of a wetting film of helium near the superfluid transition.
"Critical Fluctuation-Induced Thinning of He Films near the Superfluid Transition,"
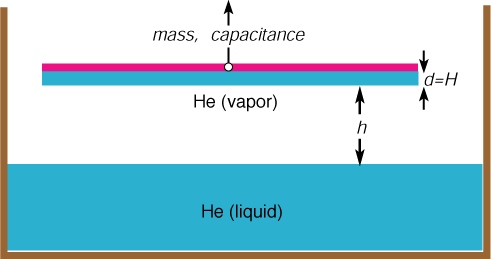
Thickness of the film (denoted by d) is obtained by minimizing its energy, as
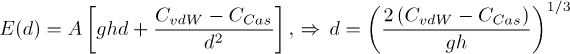
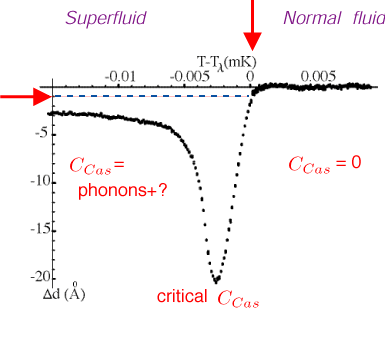
The film is thinner at the transition, and in the superfluid phase
Surface Undulations

![]() Can surface
fluctuations account for the (additional) thinning of the superfluid film?
Can surface
fluctuations account for the (additional) thinning of the superfluid film?
"Casimir Forces, Surface Fluctuations, and Thinning of Superfluid Films,"
Zandi, Rudnick, & Kardar, Phys. Rev. Lett. 93, 155302 (2004)
The normal fluid is clamped due to viscosity, while the superfluid has a velocity
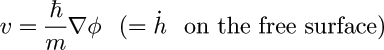
Undulations of the surface set up a superfluid velocity field that extends through the film, and vanishes at the substrate. The corresponding Hamiltonian, and free energy, give
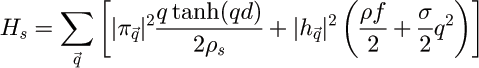
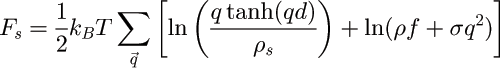
There is a corresponding force:
[Dzyaloshinskii, Lifshitz, Pitaevskii (1961); Mahale and Cole (1986)]
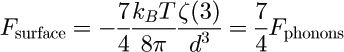
The net effect of phonons and surface undulations appear to account for the thinning of superfluid films:
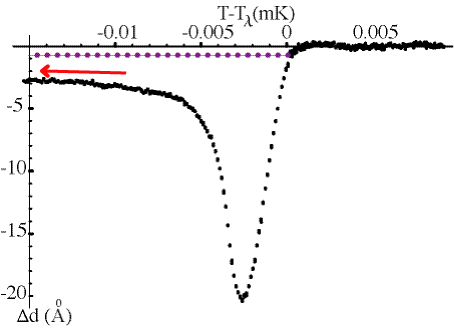
![]() Recent
results confirm collapse of scaled curves on less rough substrates:
Recent
results confirm collapse of scaled curves on less rough substrates:
"Critical Casimir force in He-4 films: Confirmation of finite-size scaling,"
Ganshin, Scheidemantel, Garcia and Chan, Phys. Rev. Lett. 97, 075301 (2006),
and explained by finite-size effects with Dirichlet boundary conditions:
Zandi, Shackell, Rudnick, Kardar, & Chayes, Phys. Rev. E 76, 030601(R) (2007).