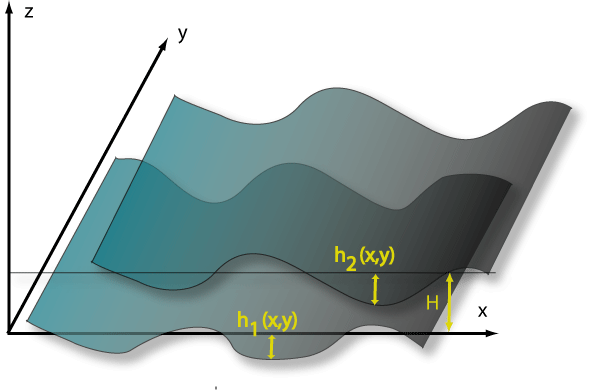
Corrugated Surfaces

Normal force
![]() A common method
for dealing with non-flat geometries is the Proximity Force
Approximation, which in effect assumes an effective Casimir interactions
between locally parallel pairs on points on the two surfaces, and sums over
all such pairs.
A common method
for dealing with non-flat geometries is the Proximity Force
Approximation, which in effect assumes an effective Casimir interactions
between locally parallel pairs on points on the two surfaces, and sums over
all such pairs.
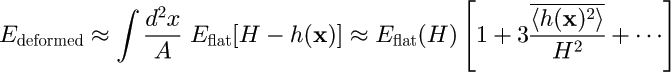
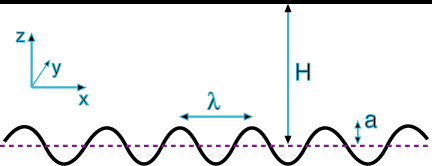
![]() For a sinusoidally
corrugated plate:
For a sinusoidally
corrugated plate:
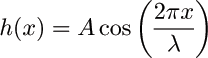
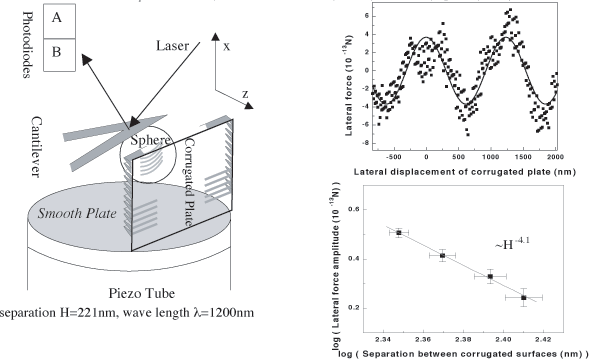
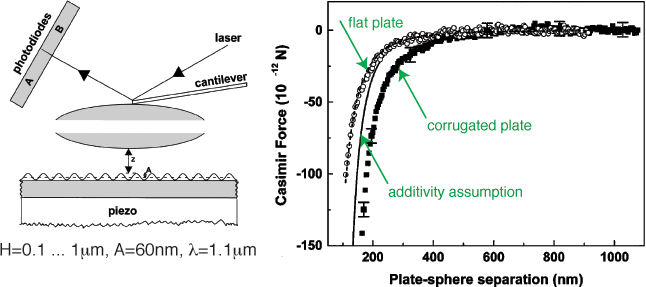
![]() "Demonstration
of the Nontrivial Boundary Dependence of the Casimir Force,"
"Demonstration
of the Nontrivial Boundary Dependence of the Casimir Force,"
Path-Integral formulation
![]() Integrate over
all configurations of the field in the space between deformed plates (or
other boundaries)
Integrate over
all configurations of the field in the space between deformed plates (or
other boundaries)
Thermal fluctuations: Scalar field with Dirichlet boundary conditions
Quantum fluctuations: EM field is equivalent to Dirichlet + Neumann in certain geometries,
TM modes (Dirichlet) + TE modes (Neumann)
![]() "Probing
the Strong Boundary Shape Dependence of the Casimir Force,"
"Probing
the Strong Boundary Shape Dependence of the Casimir Force,"
T. Emig, A. Hanke, R. Golestanian, and M. Kardar, Phys. Rev. Lett. 87, 260402 (2001)
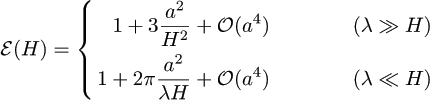
Lateral force
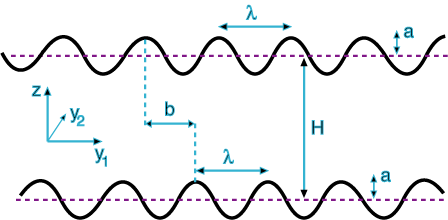
![]() A sideways
force to "align" the two plates at b=λ/2 :
A sideways
force to "align" the two plates at b=λ/2 :
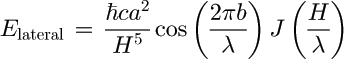
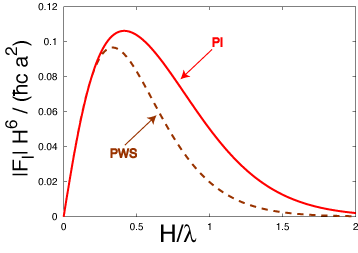
Comparison with the result of pair-wise summation:
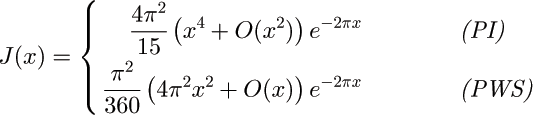
![]() "Demonstration
of the Lateral Casimir Force,"
"Demonstration
of the Lateral Casimir Force,"
F. Chen, U. Mohideen, et. al , Phys. Rev. Lett. 88, 101801 (2002)