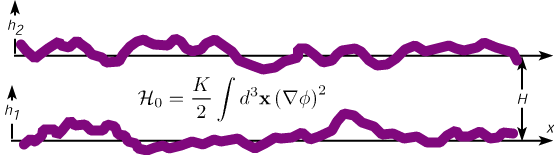
Dynamic Casimir Effects

Path-Integral formulation of Deformed boundaries

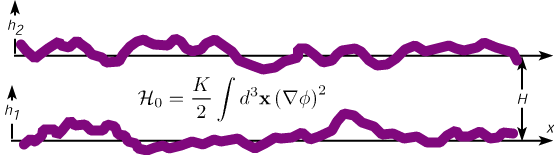
H. Li and M. Kardar, Phys. Rev. Lett. 67, 3275 (1991); Phys. Rev. A 46, 6490 (1992)  

Impose constraints on surfaces by delta-functions;

e.g. for thermal fluctuations of a scalar field with Dirichlet boundary conditions:

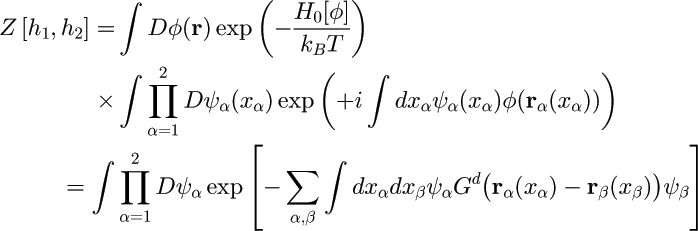
After integrating over the auxiliary field, the effective (free) energy can be obtained perturbatively in the deformations:

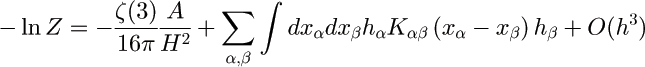
Generalization to Space-Time (4-dimensions)

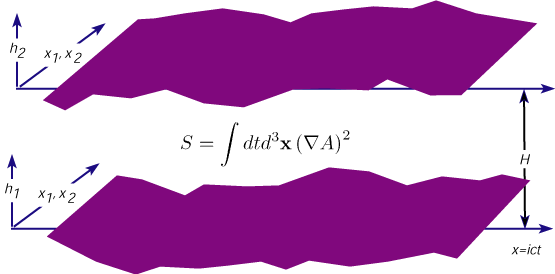
R. Golestanian and M. Kardar, Phys. Rev. Lett. 78, 3421 (1997); Phys. Rev. A 58, 1713 (1998)  

Euclidean path integral quantization of a scalar (relativistic) field:

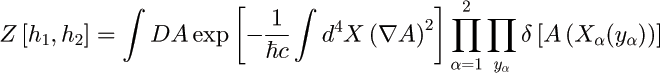
Perturbative expansion for the effective action:

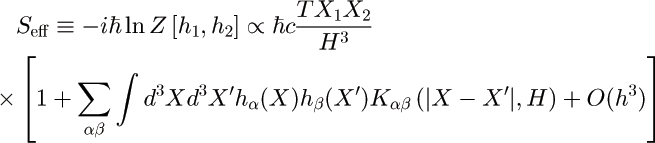
Dynamic Casimir Effects

Mechanical Response of Vacuum

The second order perturbative results from the path-integral approach, give an effective action:

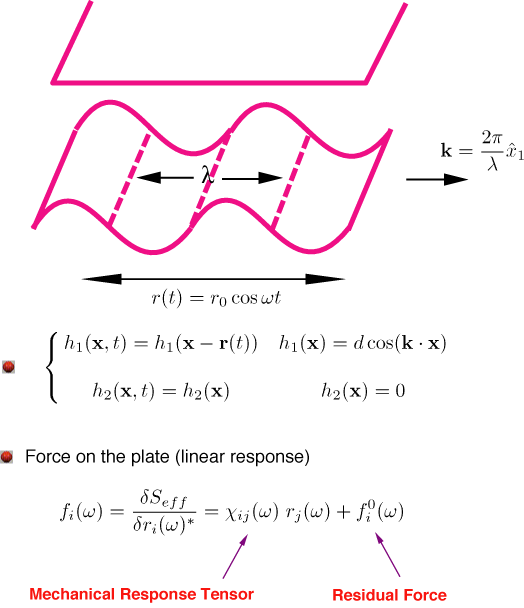
Oscillating (rocking) Plate

Let us focus on the specific case of harmonic (rocking) oscillations of a corrugated plate:

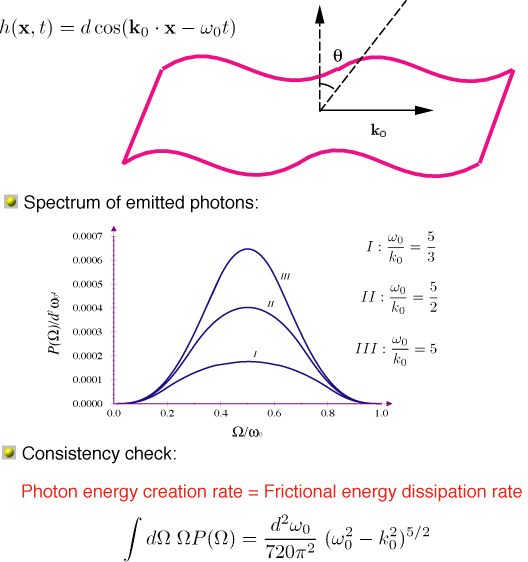
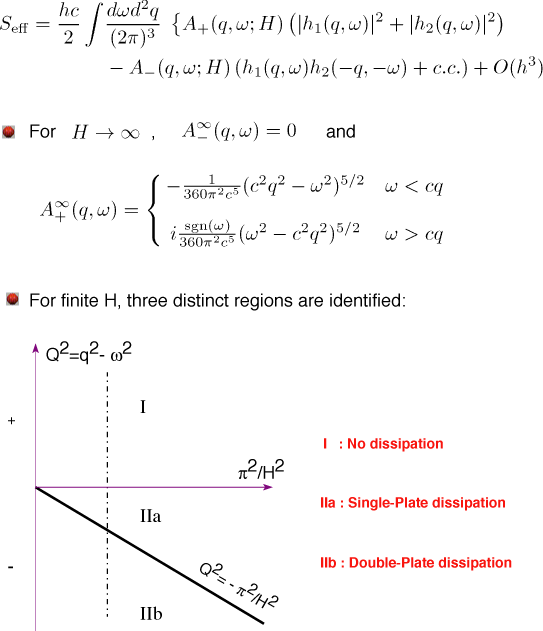
At low frequencies (ω<<ck), there are direction dependent corrections to mass!

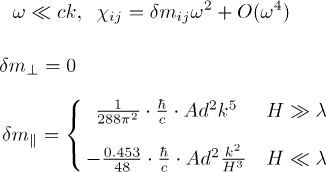
At high frequencies (ω>ck), the response function is complex, and there is frequency-dependent viscosity (dissipation):

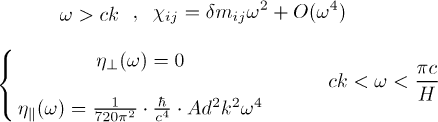
At frequencies higher than the  πc/H , the response function diverges, which we interpret as resonant dissipation by pumping the normal modes of the (no-leak) cavity.

What happens to the dissipated energy?

Radiation

"Motion-induced radiation from a dynamically deforming mirror,"

F. Miri and R. Golestanian, Phys. Rev. A 59, 2291 (1999)