Repulsion?
![]() Stiction due to the attractive Casimir force is a challenge to design and operation of MEMs.
Stiction due to the attractive Casimir force is a challenge to design and operation of MEMs.
Can Casimir forces be weakened or made repulsive? [DARPA ; Scientific American]
1. Repulsion via Boundary Conditions
![]() Scalar Fields with Dirichlet (D) or Neumann (N) boundary conditions:
Scalar Fields with Dirichlet (D) or Neumann (N) boundary conditions:
Similar boundaries (DD or NN) lead to attraction, while opposing boundaries (DN) result in repulsion.
![]() In Lifshitz (DLP) theory, this is obtained by an intervening medium with dielectric constant intermediate to the boundaries, as in the case of liquid helium climbing (wetting) a wall. (dielectric constants: solid > helium > air).
In Lifshitz (DLP) theory, this is obtained by an intervening medium with dielectric constant intermediate to the boundaries, as in the case of liquid helium climbing (wetting) a wall. (dielectric constants: solid > helium > air).
"Verification of Lifshitz theory of the van der Waals Potential using liquid-helium films,"
E.S. Sabisky and C.H. Anderson, Phys. Rev. A 7, 790 (1973)
"Measured long-range repulsive Casimir–Lifshitz forces,"
J. N. Munday, F. Capasso & V. A. Parsegian, Nature 457, 170 (2009) (gold, bromobenzene, silica)
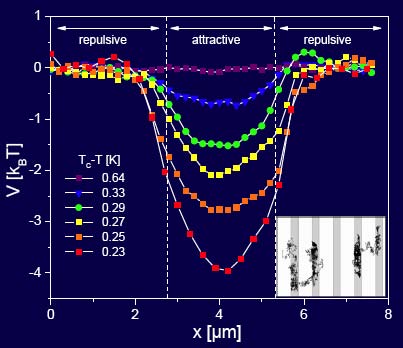
![]() Opposition of hydrophobic/hydrophilic surfaces in oil-water mixtures close to criticality:
Opposition of hydrophobic/hydrophilic surfaces in oil-water mixtures close to criticality:
"Critical Casimir forces in colloidal suspensions on chemically patterned surfaces,"
F. Soyka, O. Zvyagolskaya, C. Hertlein, L. Helden, & C. Bechinger, Phys. Rev. Lett. 101, 208301 (2008) (movie)

![]() Immersing MEMs in fluids is not practical. Is repulsion across vacuum possible?
Immersing MEMs in fluids is not practical. Is repulsion across vacuum possible?
"Van der Waals forces and zero-point energy for dielectric and permeable materials,"
T.H. Boyer, Phys. Rev. A 9, 2078 (1974) (A perfect conductor repels a perfect magnet)
A material with large permeability is required for repulsion, but in ordinary materials permeability is close to one.
Metamaterials, incorporating arrays of microengineered circuitry mimic, at certain frequencies, a strong magnetic response and have been proposed as candidates for Casimir repulsion across vacuum.

1. Repulsion via Geometry & Shape
![]() Abraham-Lorentz (+Casimir) model of electron:
Abraham-Lorentz (+Casimir) model of electron:
A spherical conducting shell of radius R , with a uniform charge e .
"Introductory remarks on quantum electrodynamics," H.B.G. Casimir, Physics 19, 846 (1956)
Casimir's "mousetrap" to catch the fine structure constant:
Balance the repulsive Coulomb energy, with the (presumed attractive) Casimir energy:
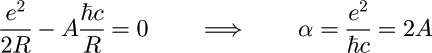
"Quantum Electromagnetic Zero-Point Energy of a Conducting Spherical Shell and the Casimir Model for a Charged Particle," T.H. Boyer, Phys. Rev. 174, 1764 (1968)
2A = - 0.09235 is negative! [also obtained by R. Balian and B. Duplantier (1977)]
"Vacuum means of energy-momentum tensor of quantized fields on manifolds of different topology and geometry. I,"
S.G. Mamaev and N.N. Trunov, Sov. Phys. J. (USA) 22, 51 (1979)
The "Casimir energy" of a parallelopiped changes sign with aspect ratio: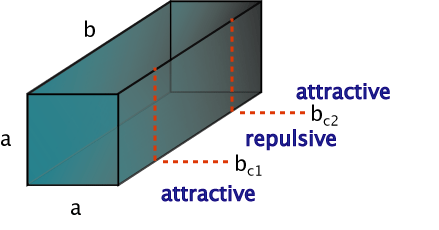
![]() Does this imply
a repulisve force?
Does this imply
a repulisve force?
"Attractive Casimir forces in a closed geometry,"
M. P. Hertzberg, R. L. Jaffe, M. Kardar, and A. Scardicchio, Phys. Rev. Lett. 95, 250402 (2005)
In the physically accessible geometry of a piston, the partition is always attracted to the closer side.
"Opposites Attract: A Theorem about the Casimir Force,"
O. Kenneth and I. Klich, Phys. Rev. Lett. 97, 160401 (2006) (two halfs of a cut sphere attract)
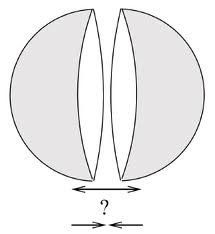
![]() Contrained repulsion?
Contrained repulsion?
"Casimir repulsion between metallic objects in vacuum,"
M. Levin, A.P. McCauley, A.W. Rodriguez, M.T.H. Reid, S.G. Johnson,Phys. Rev. Lett. 105, 090403 (2010)