Thermal non-equilibrium
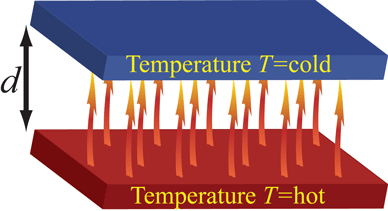
![]() Radiation Pressure from a hot-plate can in principle counteract Casimir attraction
Radiation Pressure from a hot-plate can in principle counteract Casimir attraction
 cf.
cf. 
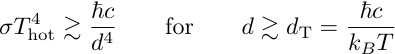
Around room temperature, this occurs for distances exceeding 7 microns; where the Casimir force is insignificant,
while at short scales "near-field effects" due to evanescent waves modify classical "Stefan-Boltzmann" law:
"Probing Planck’s Law with Incandescent Light Emission from a Single Carbon Nanotube,"
Y. Fan, S.B. Singer, R. Bergstrom, & B.C. Regan, Phys. Rev. Lett.102, 187402 (2009)

![]() A generalized scattering approach enables computation of Casimir forces, as well as radiation and heat transfer,
A generalized scattering approach enables computation of Casimir forces, as well as radiation and heat transfer,
in non-equilibrium steady states.
"Nonequilibrium Electromagnetic Fluctuations: Heat Transfer and Interactions,"
M. Krüger, T. Emig, and M. Kardar, Phys. Rev. Lett. 106, 210404 (2011)
Rytov (1959): 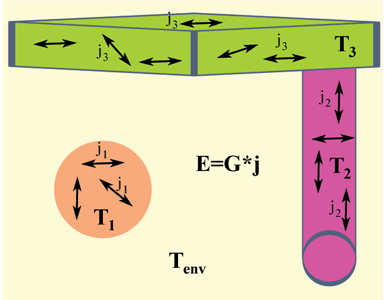 "Fluctuational QED"
"Fluctuational QED"
Fluctuating currents in each object are related to its temperature by a fluctuation-dissipation condition:
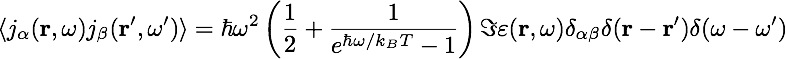
The EM field due to thermal fluctuations of one object is related to overall Green's function by:
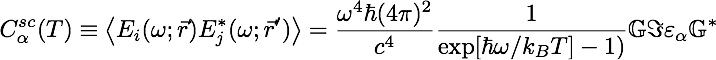
The overall fluctuations with many objects at different temperatures is then given by:
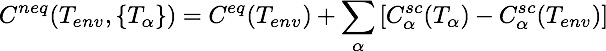
From EM correlations follow the stress tensor and the Poynting vector, hence forces and radiation.
![]() Emission from a single object (Sphere or Cylinder):
Emission from a single object (Sphere or Cylinder):
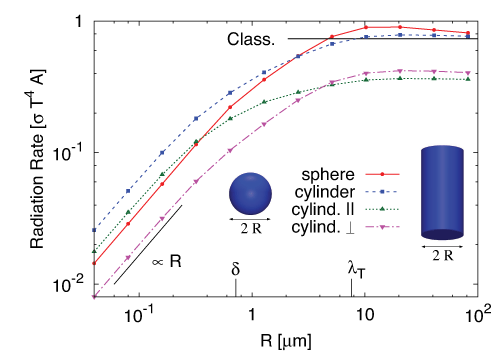
Emission is proportional to volume for small objects, crossing over to surface proportionality.
Emission from a cylinder is polarized (also switching as a function of size)
"Polarized light emission from individual incandescent carbon nanotubes,"
S. B. Singer, Matthew Mecklenburg, E. R. White, and B. C. Regan, Phys. Rev. B. 83, 233404 (2011)
"Thermalization of Heat radiation of an Individual Object Thinner than the Thermal Wavelength,"
C. Wuttke and A. Rauschenbeutel, Phys. Rev. Lett. 111, 024301 (2013)
![]() "Surface Phonon Polaritons Mediated Energy Transfer between Nanoscale Gaps,"
"Surface Phonon Polaritons Mediated Energy Transfer between Nanoscale Gaps,"
S. Shen, A. Narayanaswamy, & G. Chen, Nano Lett. 9, 2909 (2009),
(MIT news, July 29, 2009), Breaking the law at the nanoscale:
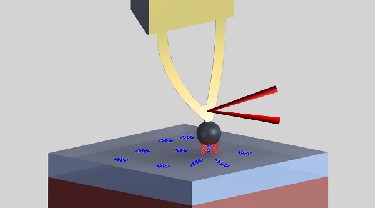
![]() Heat transfer between plates diverges at short distances due to evanescent waves (tunneling).
Heat transfer between plates diverges at short distances due to evanescent waves (tunneling).
![]() Consider forces between two spheres at different temperatures:
Consider forces between two spheres at different temperatures:
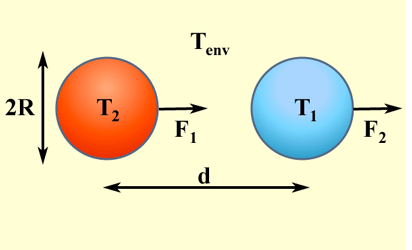
"Non-equilibrium Casimir forces: Spheres and sphere-plate,"
M. Krüger, T. Emig,G. Bimonte and M. Kardar, Europhys. Lett. 95, 21002 (2011) (1 micron Si O2 spheres, force on #2)
Whereas the equilibrium force (attractive) falls off as 1/d6, the non-equilibrium force decays as 1/d2. ( * )
The non-equilibrium force can be attractive and repulsive. ( * )
Unlike in thermal equilibrium, there are points of stable levitation. ( * )
Forces are not equal and opposite, with points of equal force in the same direction! ( * )
![]() Example of non-equilibrium Casimir levitation:
Example of non-equilibrium Casimir levitation:
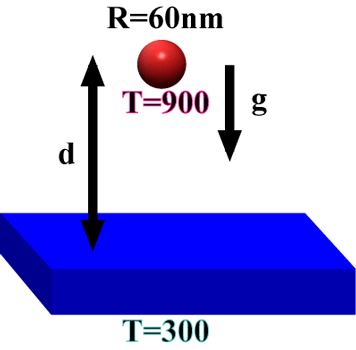
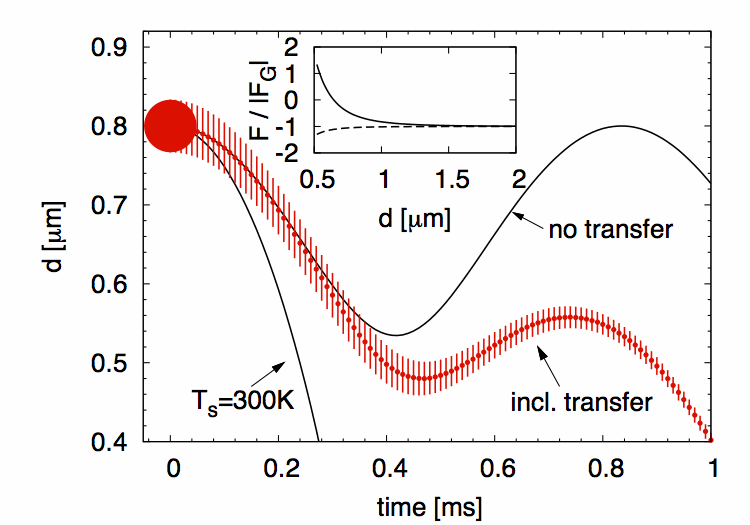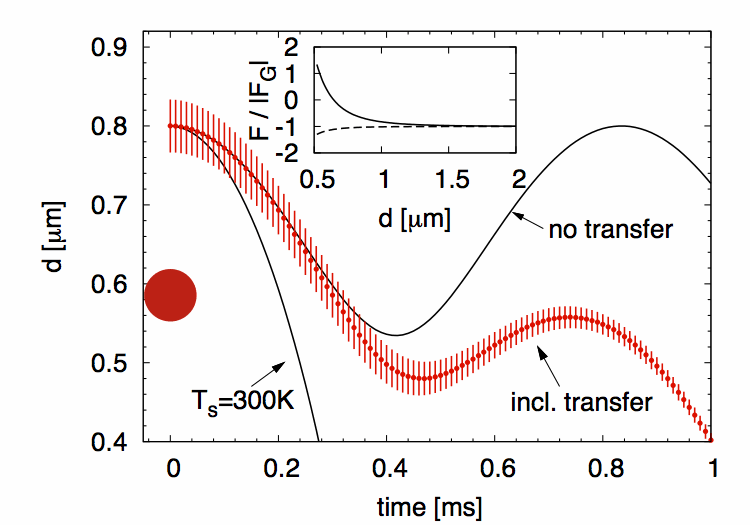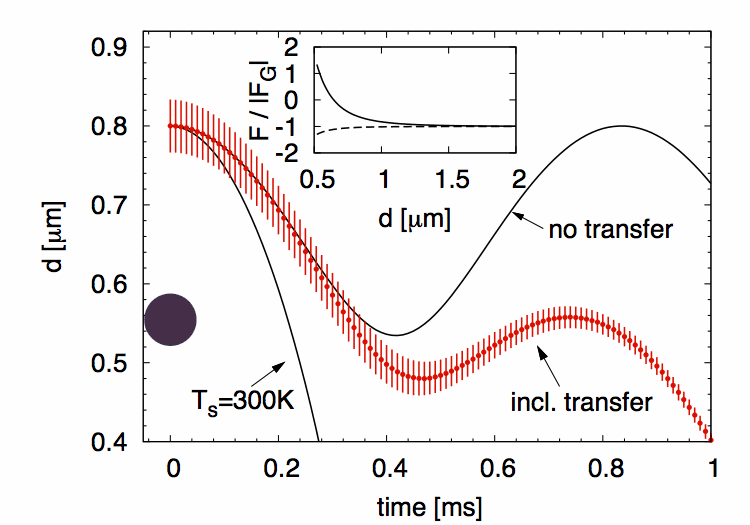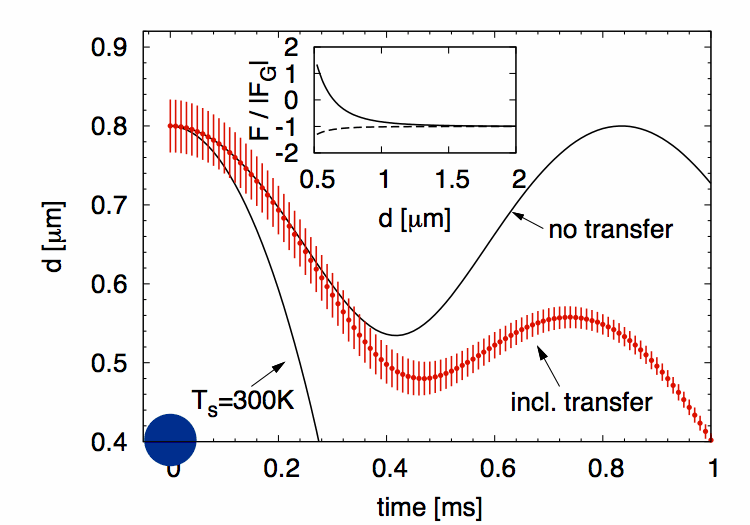
A hot microsphere can levitate on top of a cold plate.
If it cools down (including heat transfer) the sphere will fall down.