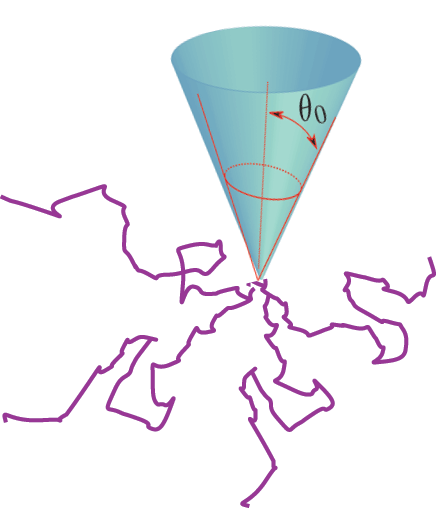
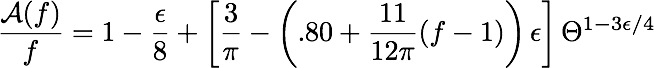Self-avoiding polymers

red ball Simulations: The dimerization method was used to generate samples of 108 SAWs on a cubic lattice,

for N =16, 32,...,1024.

yellow ball By measuring the probability that a generated SAW does not intersect the boundary, we  obtain N-Δγ

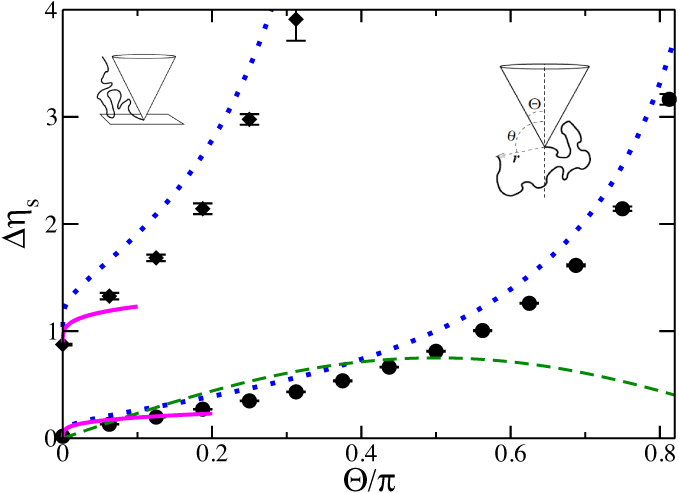
yellow ball The phantom polymer results provide an excellent approximation, except for very thin cones.

yellow ball The green dashed line is from an ε-expansion, treating the surface of the cone as a weak perturbation:

"Apex exponents for polymer-probe interactions,"

M. Slutsky, R. Zandi, Y. Kantor, M. Kardar, PRL 94, 198303 (2005)

red ball ε-expansion: A better treatment is to start with impenetrable boundaries,

along the lines of a similar computation for a wedge

"Critical behaviour at an edge," J.L. Cardy, J. Phys. A: Math. Gen. 16 3617

"Polymer-mediated entropic forces between scale-free objects,"

M. F. Maghrebi, Y. Kantor, M. Kardar, PRE 86, 061801 (2012)

yellow ball The loop-correction can only be calculated numerically in general, but for small opening angles we find

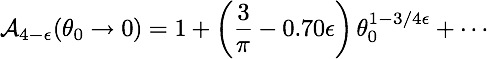
yellow ball Is the exponent for the singular dependence on angle ?

yellow ball Current simulations are not sufficient to answer this question

Many polymers

red ball  The force on a single polymer, attached to a needle, is around 0.1 pico-Newton at 0.1 micron separation.

yellow ball This force, however, can be increased by attaching many polymers to the tip.

yellow ball In the limit of small opening angle (a needle), we can utilize the large literature on star polymers:

"Statistics of many arm star polymers," K. Ohno, Phys. Rev A 40, 1524 (1989)

"Scaling theory of star polymers and general polymer networks in bulk
      and semi-infinite good solvents," K. Ohno & K. Binder, J. Phys. France 49, 1329 (1988)

yellow ball At the lowest order in ε-expansion, the force is simply multiplied by the number of polymers;

corrections are expected at higher orders, with the force increasing faster than linearly (as f 3/2 ?)