Affinity Maturation of B cells
![]() Following infection, B cell receptors are released as Antibodies targeting specific pathogens (Antigens)
Following infection, B cell receptors are released as Antibodies targeting specific pathogens (Antigens)
Antibodies mature the in Germinal Centers in lymph nodes:
Computational Model:
![]() The processes of (hyper)mutation/competition/selection lead to rapid Population Evolution:
The processes of (hyper)mutation/competition/selection lead to rapid Population Evolution:
Fitness f governs reproduction rates according to
Population mean is defined by
Mean fitness evolves as
Affinity ω is a trait correlated with fitness, and (including possibility of mutations) evolves as
![]() To use the
To use the ![]() equations in Affinity Maturation, we need to describe the dependence of fitness on affinity.
equations in Affinity Maturation, we need to describe the dependence of fitness on affinity.
![]() Vaccination with synthetic nano-particles coated with target antigens:
Vaccination with synthetic nano-particles coated with target antigens:
Is there an optimal density n for coated target antigens?
Fitness of the maturing B cells depends on receptor affinity ω, and spike density n, say as:
![]()
Approximating the affinity distribution by a Gaussian of mean
and variance
, Price's equation leads to
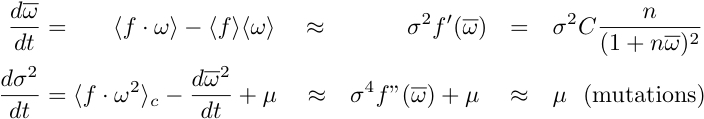
With these approximations, the equations are easily integrated to yield:
where ![]() , and
, and ![]() .
.
![]() In a variety of models, optimal affinity is achieved at an intermediate target density:
In a variety of models, optimal affinity is achieved at an intermediate target density:
Optimal affinity is achieved at target (spike) density of less than ~1 per area spanned by the BC:
too few targets at low density to be productive, too many targets at high density to be competitive.
![]() The low spike density of HIV may have evolved because of the effects of T helper cell depletion on affinity maturation
The low spike density of HIV may have evolved because of the effects of T helper cell depletion on affinity maturation
A. Amitai, A.K Chakraborty, and M. Kardar, PLOS Computational Biology (2018) (offline)
![]() Broadly neutralizing Antibodies.
Broadly neutralizing Antibodies.