Add an additonal cost from epitopes targeted by the host immune system (mostly T cells for HIV):
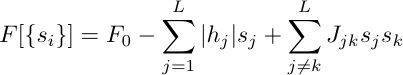
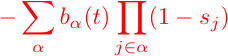
Use the equations to compute the time evolution of single site mutation probabilities
,
where the `mean-field approximation' from statistical physics gives
The essence of the `mean-field approximation' is the neglect of the correlations betweem sites, setting
Such `linkage equilibrium' is achieved in population genetics if the sequence elements are completely reshuffled post replication, i.e. for infinite recombination rate [Neher & Shraiman, Rev. Mod. Phys. 83, 1283 (2011)] (offline)
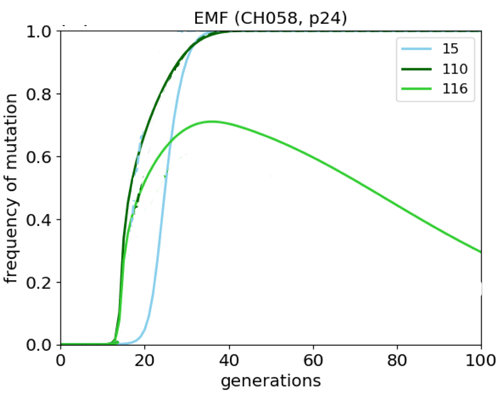
How well does this approach work in an actual patient?
Assume a fitness landscape for viral sequence (single protein or whole genome), [binary (0 for consensus, 1 for mutant) of length L] including one site and two site terms.
equations to compute the time evolution of single site mutation probabilities
,where the `mean-field approximation' from statistical physics gives
=h_i.jpeg)
_pro.jpeg)
vs. 
