Self-avoiding polymer

 Simulations: The dimerization method was used to generate samples of 108 SAWs on a cubic lattice,

for N =16, 32,...,1024.

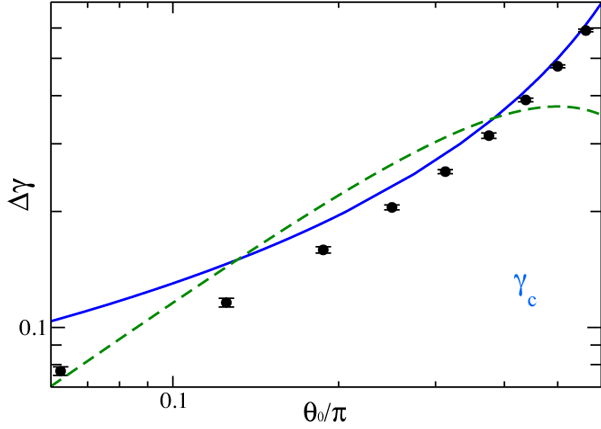
 By measuring the probability that a generated SAW does not intersect the boundary, we  obtain N-Δγ

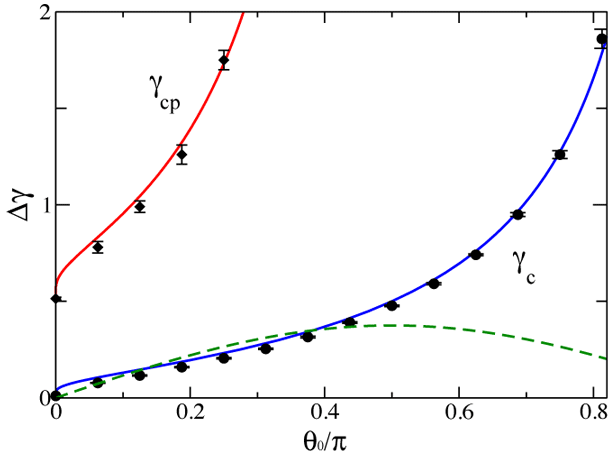
 The phantom polymer results provide an excellent approximation, except for very thin cones.

 The green dashed line is from an ε-expansion, treating the surface of the cone as a weak perturbation:

"Apex exponents for polymer-probe interactions,"

M. Slutsky, R. Zandi, Y. Kantor, M. Kardar, PRL 94, 198303 (2005)

 ε-expansion: A better treatment is to start with impenetrable boundaries,

along the lines of a similar computation for a wedge

"Critical behaviour at an edge," J.L. Cardy, J. Phys. A: Math. Gen. 16 3617

 The loop-correction can only be calculated numerically in general, but for small opening angles we find

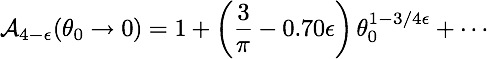
 Is the exponent for the singular dependence on angle ?

 Current simulations are not sufficient to answer this question