Self-avoiding polymer
![]() Simulations: The dimerization method was used to generate samples of 108 SAWs on a cubic lattice,
Simulations: The dimerization method was used to generate samples of 108 SAWs on a cubic lattice,
for N =16, 32,...,1024.
By measuring the probability that a generated SAW does not intersect the boundary, we obtain N-Δγ
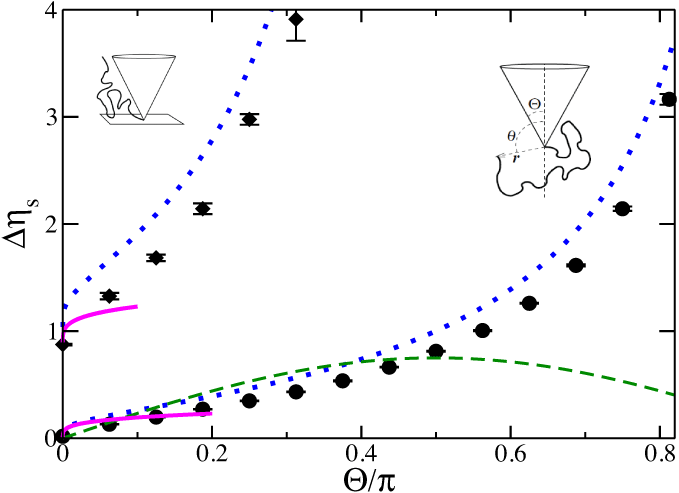
The phantom polymer results provide an excellent approximation, except for very thin cones.
The green dashed line is from an ε-expansion, treating the surface of the cone as a weak perturbation:
"Apex exponents for polymer-probe interactions,"
M. Slutsky, R. Zandi, Y. Kantor, M. Kardar, PRL 94, 198303 (2005)
![]() ε-expansion: A better treatment is to start with impenetrable boundaries,
ε-expansion: A better treatment is to start with impenetrable boundaries,
along the lines of a similar computation for a wedge
"Critical behaviour at an edge," J.L. Cardy, J. Phys. A: Math. Gen. 16 3617
"Polymer-mediated entropic forces between scale-free objects,"
M. F. Maghrebi, Y. Kantor, M. Kardar, PRE 86, 061801 (2012)
The loop-correction can only be calculated numerically in general, but for small opening angles we find
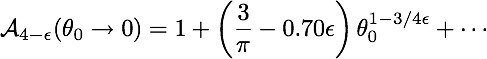
Is the exponent for the singular dependence on angle
?
Current simulations are not sufficient to answer this question