Engine

Radiation and force from a heated ratchet:

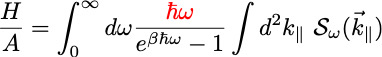
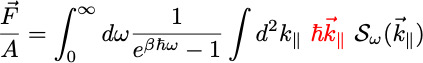
"Near Field Propulsion Forces from Nonreciprocal Media," D. Gelbwaser, N. Graham, M. Kardar, M. Krüger,

Phys. Rev. Lett. 126, 170401 (2021).

Dispersion relation of photons (relevant at far fields):      

Reciprocity of electromagnetic field equations:            

"Nonreciprocal radiative heat transfer between two planar bodies," L. Fan, ..., C. Fan, PRB 101, 085407 (2020).

 The reciprocity condition can be broken in a number of ways, e.g. by magneto-optical coupling

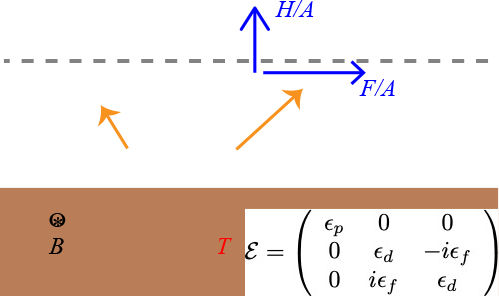
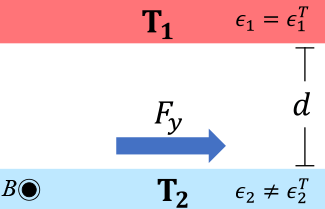
There is a propulsive force in a magnetic field, which can be used to construct a heat engine

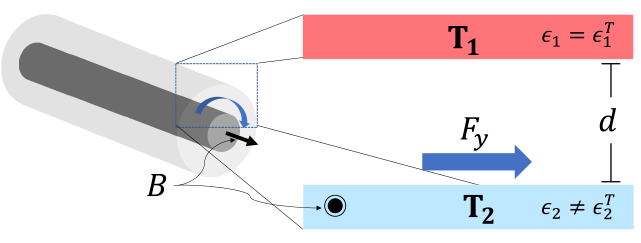
Both heat transfer and propulsive force are larger in the near-field regime , where    is a characteristic material frequency.

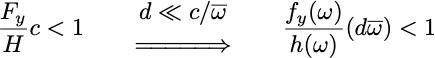
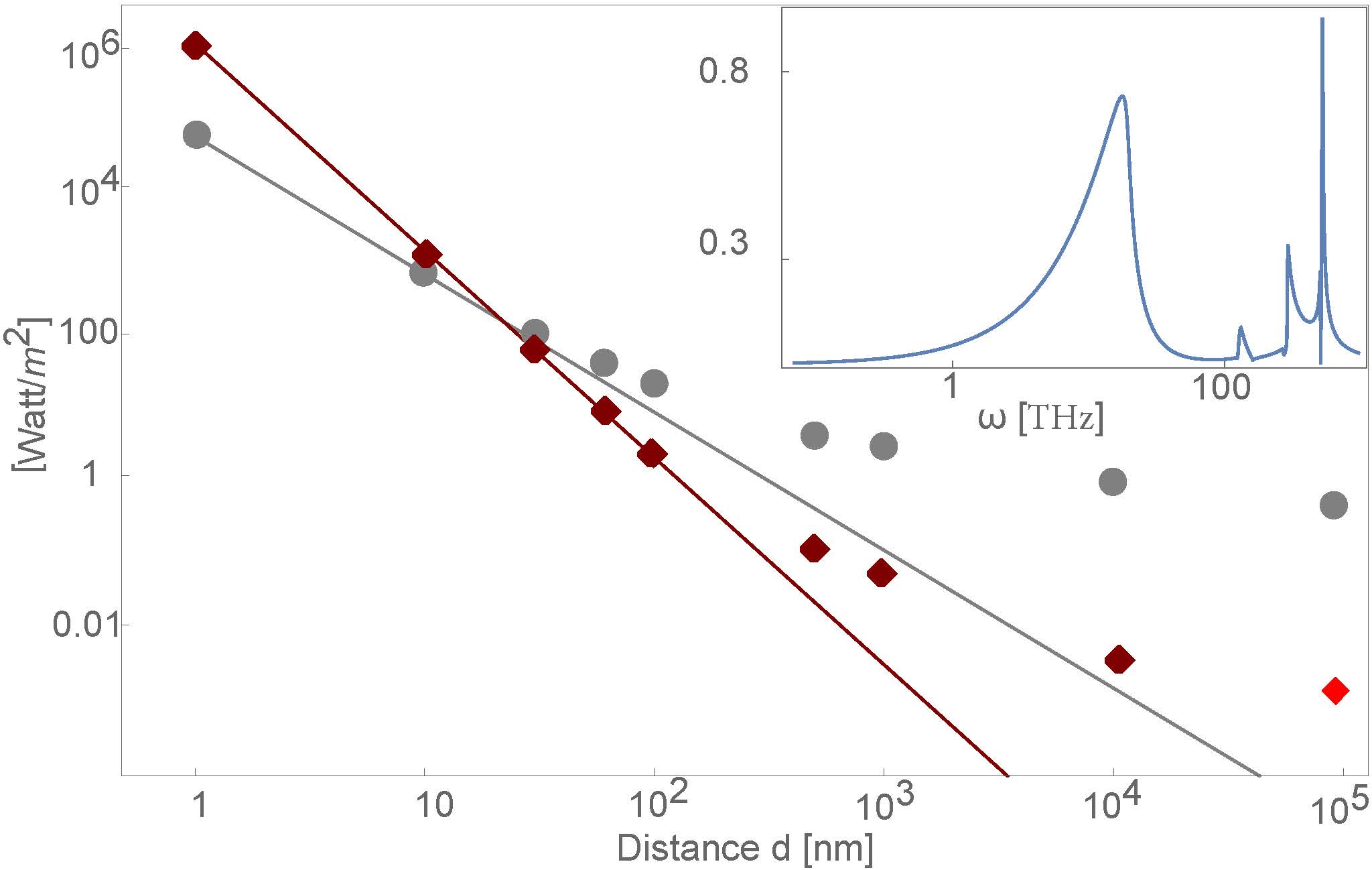
Scaled motive force F (red diamonds), and heat transfer H (gray circles) for a SiC plate and one of n-InSb subject to a magnetic field along the x-axis. The dots correspond to numeric calculations and the continuous lines to the small d asymptotes. Note that the force changes sign from +y to -y (dark red to light red diamond) at large separation. Inset: [f(ω)/h(ω)](ωd) for d= 1nm.

(Figure parameters: B= 10T, T1= 300K, T2= 270K.)

 Near field: For simplicity, let us consider a material with a single dominant frequency   , where the propulsive force and heat transfer in the near-field regime can be estimated as

where C  is dimensionless, and  is a measure of asymmetry, e.g.  in a magnetic field.

 Work can be extracted from the motive force, only if the plate is moves with some velocity v

From the extracted power, the engine efficiency is given by

What prevents this efficiency to exceed the Carnot efficiency?

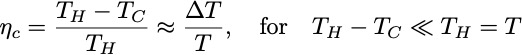
A naive interpretation of the above formula is that the Carnot efficiency is exceed for velocities greater than

Onsager relations, however, imply that if heat exchange drives motion, motion must modify heat exchange according to

while there are also frictional forces (even with a vacuum gap) reducing the propulsive force to

,  with 

This leads to a final expression for the efficiency of

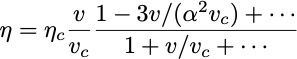
For maximum power

Next (Summary) Outline Casimir force Work extraction Fluctuational QED Engine Summary