Phase separation and disorder

 Interacting active particles (with or without attraction) can undergo Motility Induced Phase separation (MIPS):

         

  What happens to this phase transition if active particles move on a random (short-range correlated, bounded) landscape?

Sunghan Ro, Y. Kafri, M. Kardar, J. Tailleur, Phys. Rev. Lett. 126, 048003 (2021)

yellow ball For non-interacting active particles, density variations are similar to that expected for an equilibrium system

in response to a chemical potential (magnetic field) with long-range correlations:

yellow ball We may inquire of the effects of a similar "random field" on phase transition of an equilibrium system:

  Imry-Ma: Consider stability of an ordered domain of size  R to flip to the oppositely ordered state;

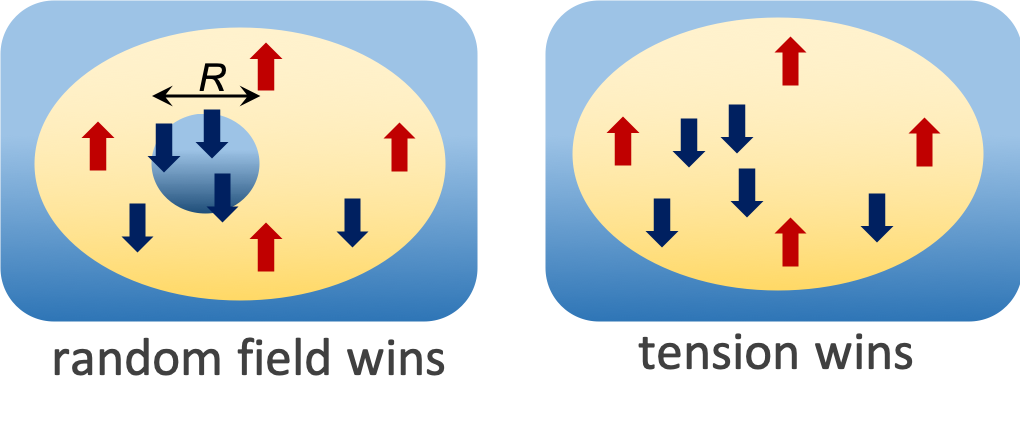
yellow ball Can the cost of surface tension be made up by a fortuitous gain in random field energy?

The ordered phase is unstable to random field induced flips of large enough domains for

yellow ball The absence of MIPS with disorder is supported by simulations:

Quench with no disorder:

Quench with bulk disorder:

 

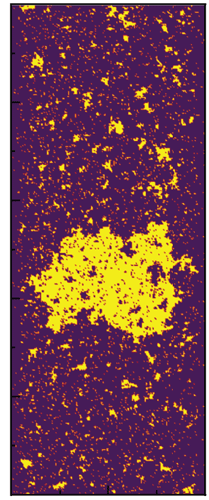
yellow ball Turning on bulk disorder in a phase separated state:

yellow ball Turning off bulk disorder:

 Disorder on boundaries is surprisingly sufficient to destroy phase separation (order) in the bulk!

yellow ball Local random asymmetries at the boundary acts as pumps that stir up the interior of the active fluid over long distances.

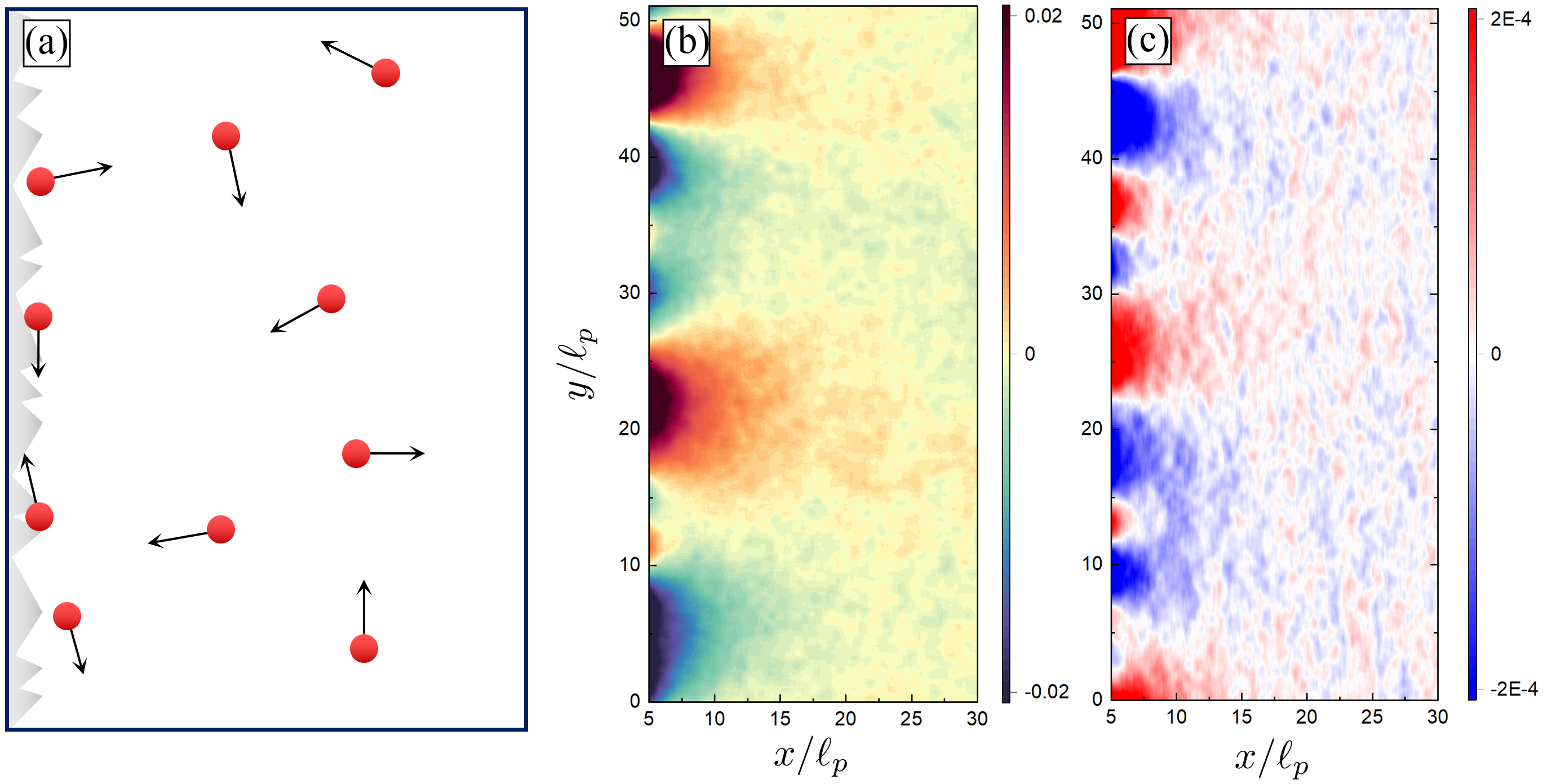
(a)  Simulation setup                                             (b) Density fluctuations            (c) Current fluctuations (y-direction)

yellow ball Imry-Ma argument can be generalized to include the effect long-range fields sourced at a boundary

The ordered phase in the bulk is unstable to boundary field induced flips of large enough domains for

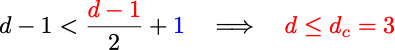
  Passive flat wall:     Active flat wall:    

Passive rough wall:   Active rough wall: 

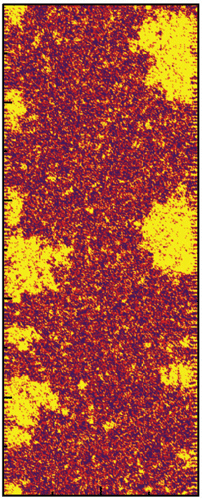
yellow ball Turning on boundary disorder in a phase separated state:

Ydan Ben Dor, S. Ro, Y. Kafri, M. Kardar, J. Tailleur, Phys. Rev. E 105, 044603 (2022)