Pressure of Active Matter
Active matter? Some examples:
Self-propelled colloidal particles Swimming Cells
Shaken Grains
What is the Pressure of an Active particle fluid? Does it behave like an equilibrium system?
A. P. Solon, J. Stenhammar, R. Wittkowski, M. Kardar, Y. Kafri, M. E. Cates, J. Tailleur, Phys. Rev. Lett. 114, 198301 (2015);
A. P. Solon, Y. Fily, A. Baskaran, M. E. Cates, Y. Kafri, M. Kardar, J. Tailleur, Nature Phys. 11, 673 (2015)
Two common models are Run and Tumble Paticles (RTP), and Active Brownian Particles (ABP):
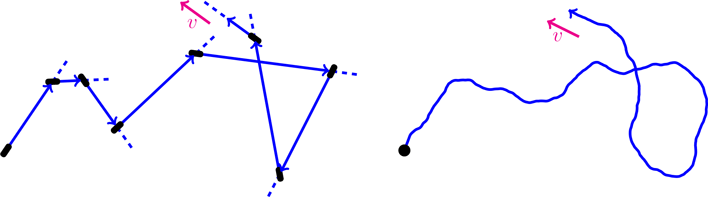
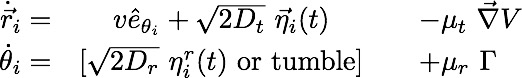
Force and pressure can be measured by introducing a wall potential:
Reorientation of an active particle close to the wall needs to be separately specified:
Pressure depends on the wall potential - No equation of state!
For non-interacting ellipses, pressure decreases whe the torque increases:
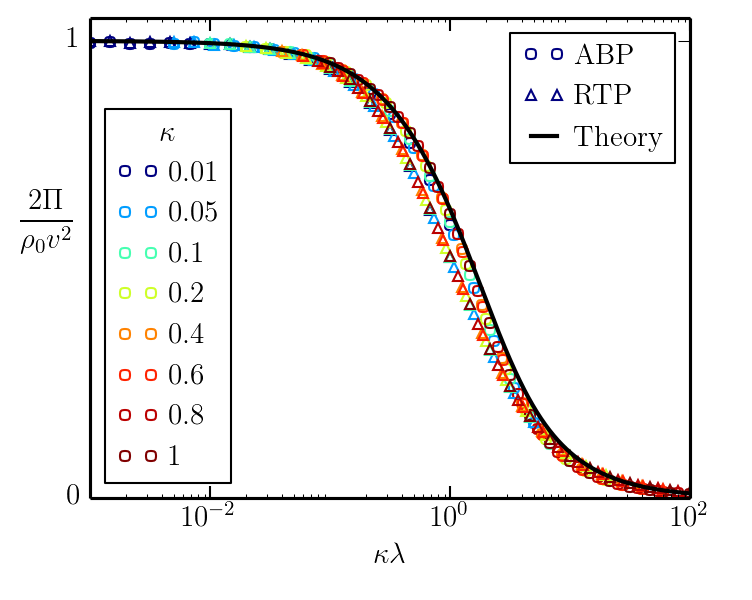
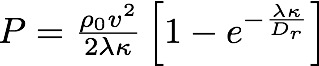
There is a net force on a closed box. (Note that there is no momentum conservation.)
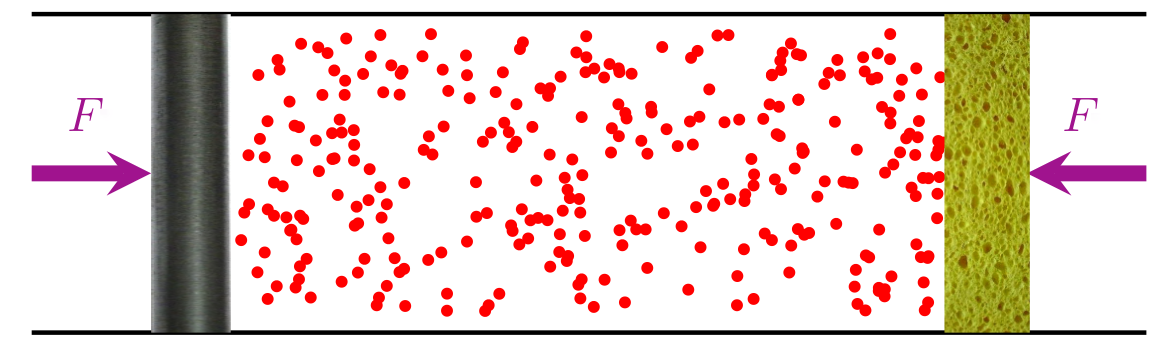vs.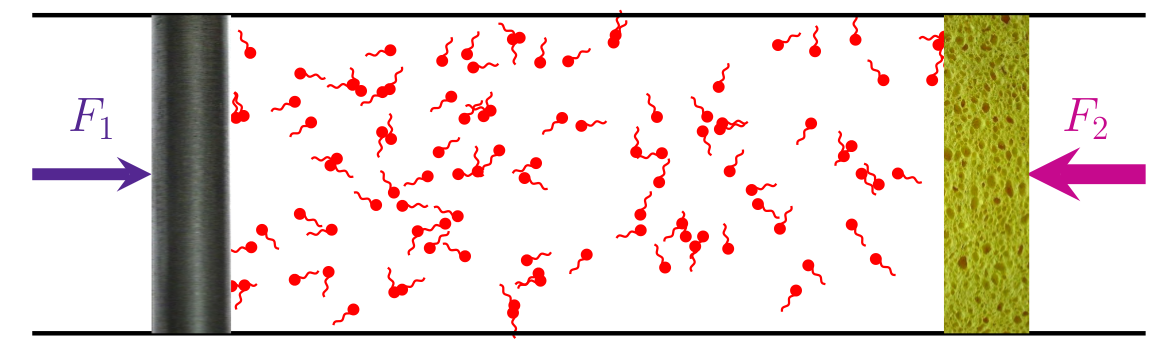
In the absence of external torques, averaging active particle equations of motion gives:
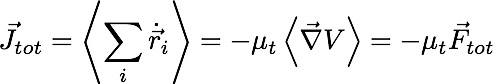
For a closed box the total force and current will both be zero independent of wall potential.
Are there any remaining surprises in the absence of reorientation (toque) at the wall? E.g. due to
Wall shape and curvature:
N. Nikola, A.P. Solon, Y. Kafri, M. Kardar, J. Tailleur, R. Voiturie, Phys. Rev. Lett. 117, 098001 (2016);
Tangential Ratchet force: Asymmetric walls support a current and net tangential force:
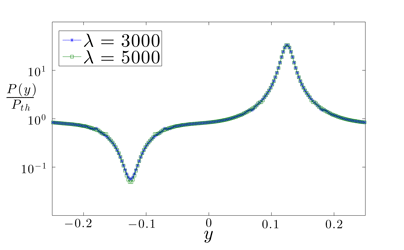
Normal force variations for sinusoidal wall: 
(Density is non-uniform, depending on curvature as well as potential)
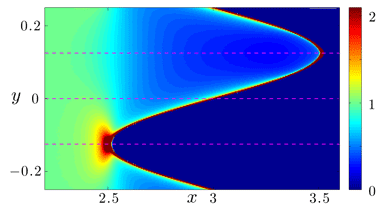
Activity-induced line/surface tension?
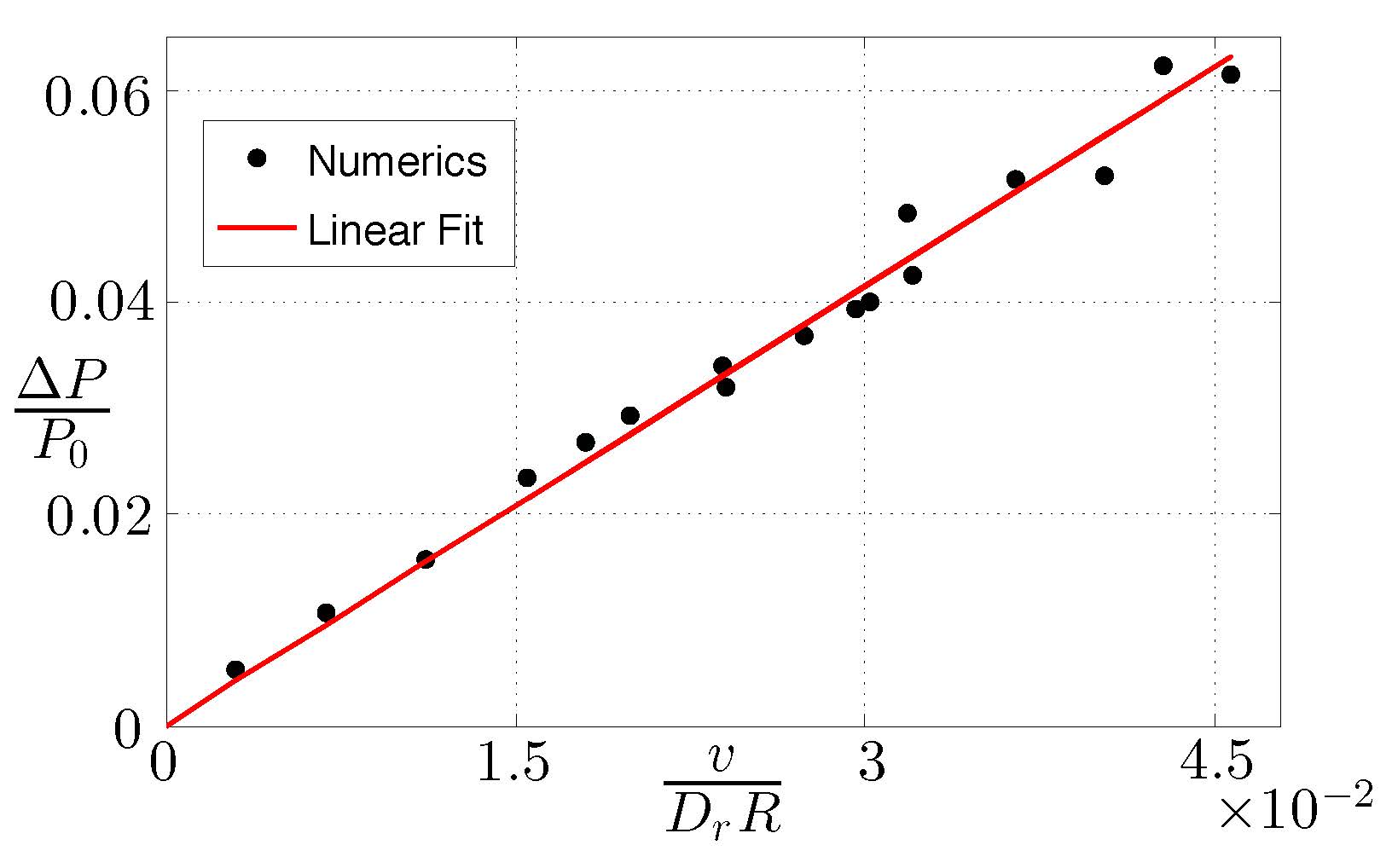
The dependence of pressure on curvature is reminiscent of Laplace's law:
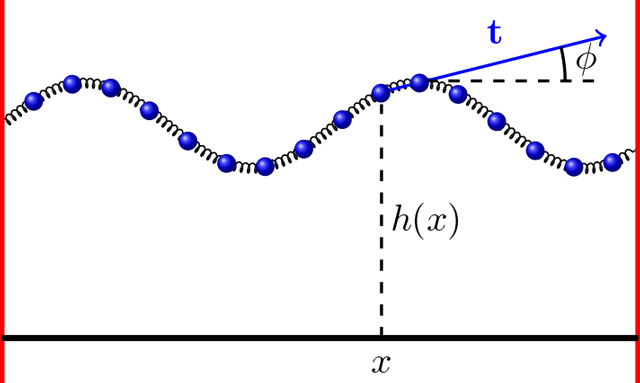
Bendable soft boundary:
Reduction in line tension lead to modulational instability:
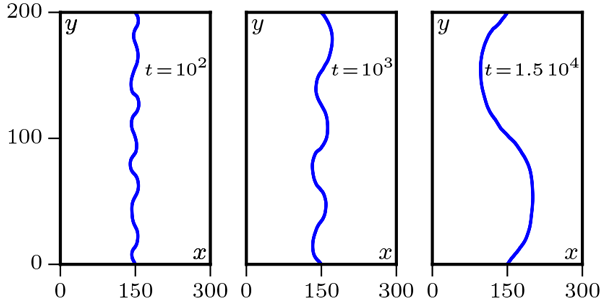
A granular chain subject to active particles (Olivier Dauchot, ESPCI)
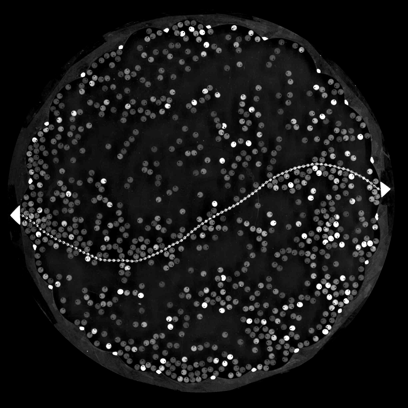
A flexible chain (worm) spontaneously curves and moves: