Pressure of Active Matter
Active matter? Some examples:
Self-propelled colloidal particles Swimming Cells
Shaken Grains
What is the Pressure of a Gas of Active particles? Does it behave like an equilibrium system?
A.P. Solon, J. Stenhammar, R. Wittkowski, M.K., Y. Kafri, M.E. Cates, J. Tailleur, PRL 114, 198301 (2015)
A. P. Solon, Y. Fily, A. Baskaran, M. E. Cates, Y. Kafri, M. Kardar, J. Tailleur, Nature Phys. 11, 673 (2015)
Two common models are Run and Tumble Paticles (RTP), and Active Brownian Particles (ABP):
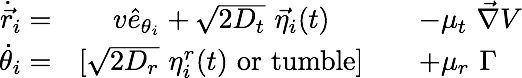
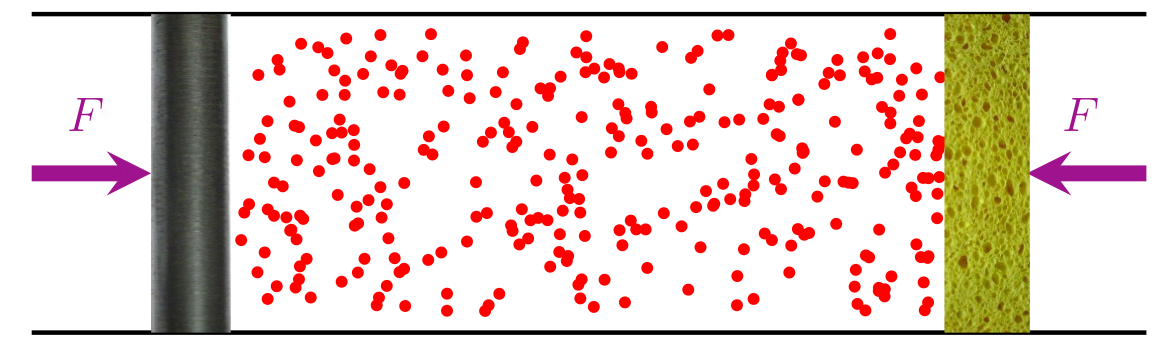
Force and pressure can be measured by introducing a wall potential:
Reorientation of an active particle close to the wall needs to be separately specified:
Pressure depends on the wall potential - No equation of state!
There is a net force on a closed box. (Note that there is no momentum conservation.)
vs.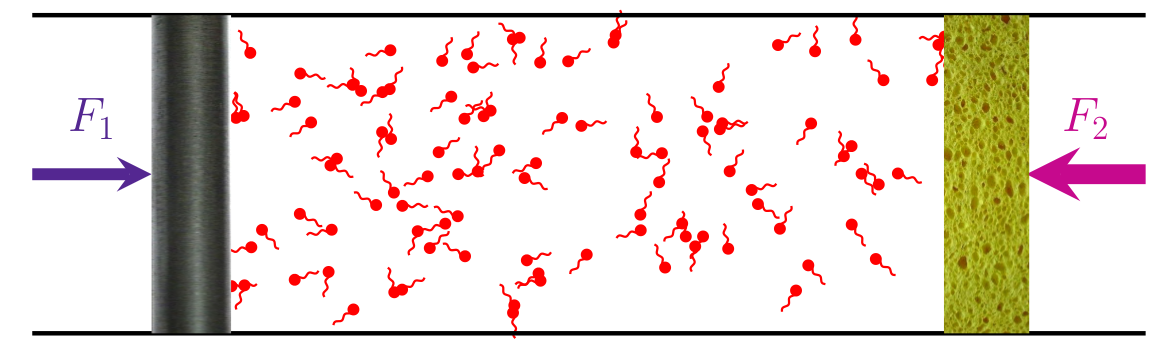
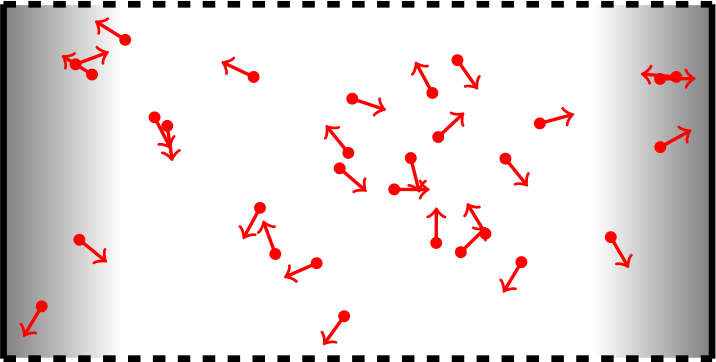
In the absence of external torques, averaging active particle equations of motion gives:
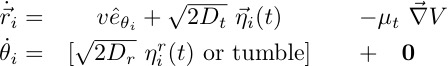
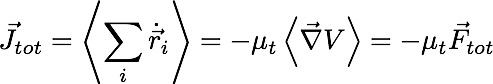
For a closed box the total force and current will both be zero independent of wall potential.
Are there any remaining surprises in the absence of reorientation (toque) at the wall? E.g. due to
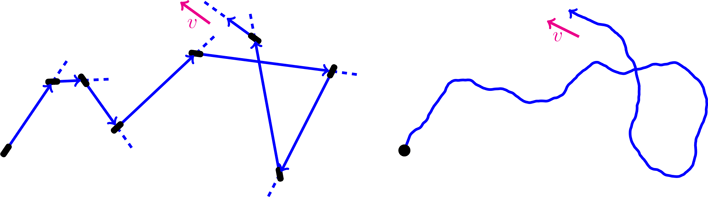
Wall shape and curvature:
N. Nikola, A.P. Solon, Y. Kafri, M. Kardar, J. Tailleur, R. Voiturie, PRL 117, 098001 (2016);
Tangential Ratchet force: Asymmetric walls support a current and net tangential force:
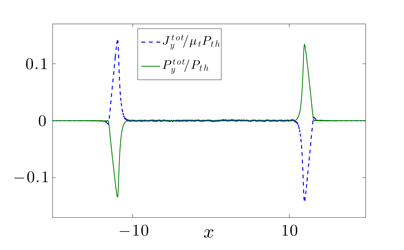
Normal force variations for sinusoidal wall:
(Density is non-uniform, depending on curvature and potential)
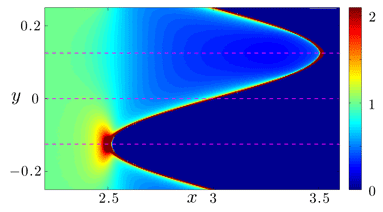
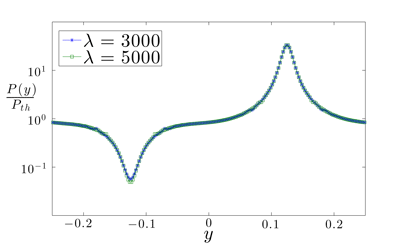
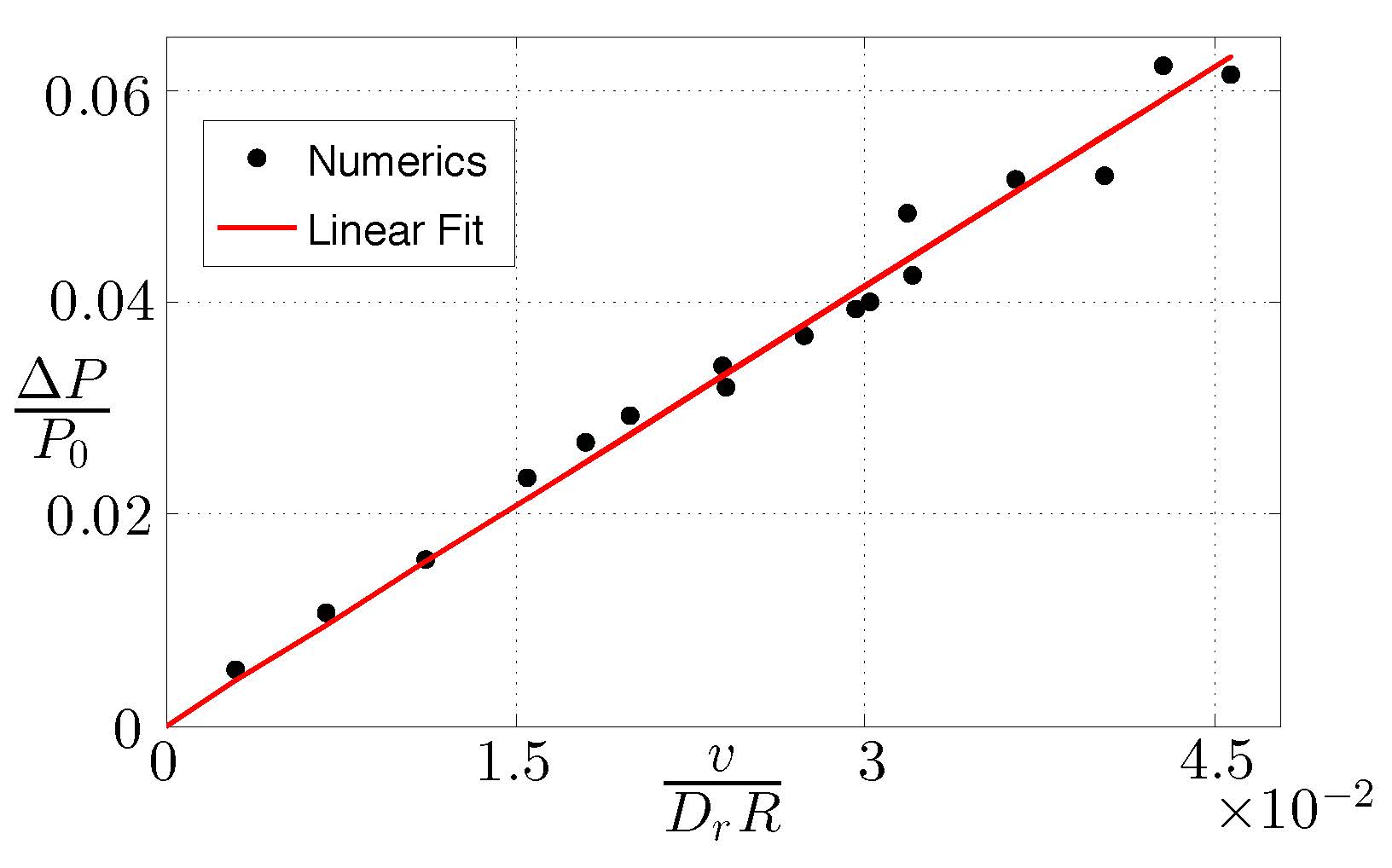
The dependence of pressure on curvature is reminiscent of Laplace's law
Activity-induced line/surface tension 
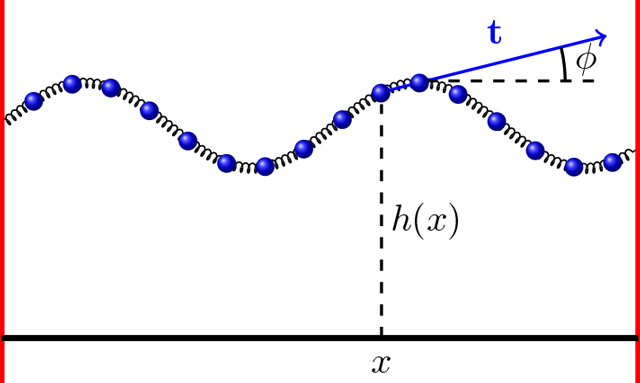
Bendable soft boundary:
Reduction in line tension leads to modulational instability:
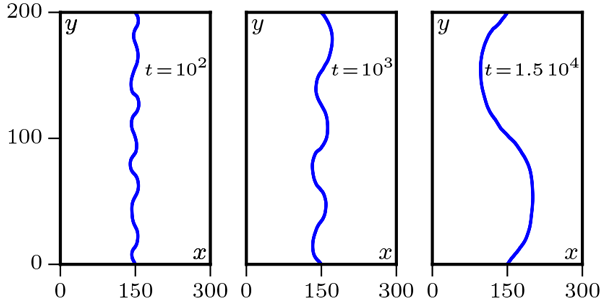
Confirmation for a granular chain held on a vibrating plate of shaken particles (Physics Viewpoint)
G. Junot, G. Briand, R. Ledesma-Alonso, and O. Dauchot, PRL 119, 028002 (2017)
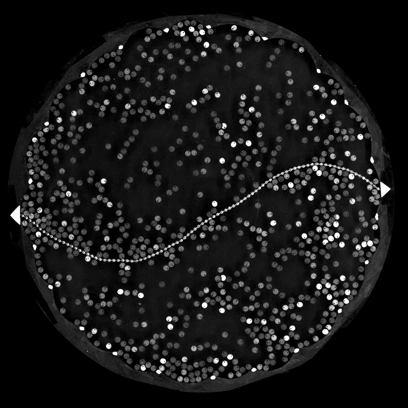
A flexible chain (worm) spontaneously curves and moves:
Active particles at a boundary exert non-intuitive normal (pressure) and tangential (ratchet) forces.