Dynamic Casimir Phenomena
![]() Accelerating bodies in vacuum may experience friction, and emit radiation.
Accelerating bodies in vacuum may experience friction, and emit radiation.
"Quantum Theory of the Electromagnetic Field in a Variable-Length One-Dimensional Cavity,"
G. T. Moore, J. Math. Phys. 11, 2679 (1970)
"Radiation from a Moving Mirror in Two Dimensional Space-Time: Conformal Anomaly,"
S. A. Fulling and P. C. W. Davies, Proc. R. Soc. London, Ser. A 348, 393 (1976).
![]() Rotating Steady State: A dielectric sphere rotating with angular frequency Ω
Rotating Steady State: A dielectric sphere rotating with angular frequency Ω

Consider waves of frequency ω and angular state m :
Lab frame:
Object frame:
"Generation of waves by a rotating body," Ya B. Zel'dovich, JETP Lett. 14, 180 (1971);
If ω'and ω have opposite signs:
Amplitude of (classical) scattered wave exceeds incoming wave (Super-radiance).
Conjectured (quantum) spontaneous emission with no incoming wave.
"Spontaneous emission by rotating objects: A scattering approach,"
M.F. Maghrebi, R.L. Jaffe, & M. Kardar, PRL108, 230403 (2012).
Number of photons in a mode of frequency ω and angular state m,
generated by object rotating with angular velocity Ω is:
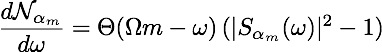
E.g., net power for a rotating cylinder:
![]() Force fluctuations: Dissipation implies fluctuations; all forces discussed so far are averages of a fluctuating quantity.
Force fluctuations: Dissipation implies fluctuations; all forces discussed so far are averages of a fluctuating quantity.
As a simple consequences of such fluctuations consider the wanderings of
a classical particle of mass m in a quantum bath.
There is no net force on the particle, but it disperses due to force fluctuations:
Langevin equation for an otherwise free particle,
In the commonly used Caldeira-Legget formalism, the force is linearly coupled to the bath,
However, a linear coupling is forbiddent for a neutral, but polarizable, particle.
With linear coupling, a free field theory implies a Gaussian distribution for φ,
hence the force and the displacement are also Gaussian distributed, entirely described by the variance
For a neutral particle (no linear coupling), the quadratic force is not Gaussian distributed; leading to cumulants
consistent with a power-law probability distribution, reminiscent of Levy flights:
Potential realizations for solitons in Bose-Einstein condensate.
Fluctuational QED predicts unexpected phenomena out of equilibrium.