Competition, mutation, & extinction on a rough front

red ball Competitive reproduction (fitness) and mutation of two species, say A and B:

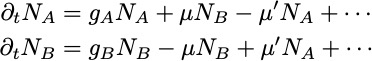
yellow ball Fraction   f   of A particles changes as

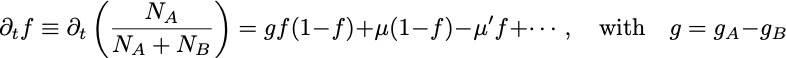
yellow ballDiffusion and and stochasticity in reproduction (so-called demographic noise) broadens the above to

In the absence of mutations,   f=0  and   f=1 are absorbing states.

With μ=0  there is a phase transition to the absorbing state  f=0 from an active state with

yellow ballExtinction of the active phase (to  f=0) belongs to the Directed Percolation universality class, described by the field theory

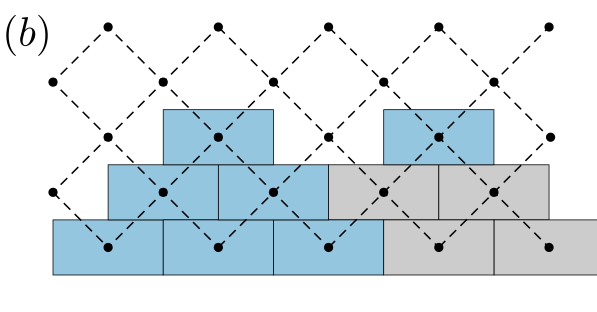
Layer by layer growth (each layer regarded as time slice) provides an example of this transition

            

yellow ball How is this formulation modified for extinction at the rough front of range expansion?

                

yellow ball In the same way that the local expansion velocity depends on local shape (through curvature and slope)

Competitive growth and mutation rates could depend upon local front shape (its curvature and slope):

The expansion velocity, conversely, could depend upon local composition through   f :

red ball The extinction transition in range expansion with a rough front, can be studied systematically by

including the lowest order couplings in a gradient expansion between height and concentration fluctuations, leading to

    

yellow ball"Bacterial range expansions on a growing front: Roughness, Fixation, and Directed Percolation,"

J. Horowitz & M. Kardar PRE 99, 042134 (2019) (off-line)

Related equations were proposed and studied in connection with binary alloy ordering for a growing film:

"Interplay between phase ordering and roughening on growing films,"

B. Drossel & M. Kardar, Eur. J. Phys. B 36, 401 (2003)  (off-line)

yellow ballNon-linear terms are relevant below 4 dimensions, different criticality from standard directed percolation expected.

Renormalization group flows are to strong coupling, with no pertinent fixed point perturbatively accessible.