Growth Morphologies
![]() Competing variants would generically expand at different rates.
Competing variants would generically expand at different rates.
The bulging circular arc is a common morphology for growth of a fitter mutant:
"Selective sweeps in growing microbial colonies,"
K.S. Korolev, M.J.I. Muller, N, Karahan, A.W. Murray, O. Halatschek, D.R. Nelson, Phys. Biol 9, 026008 (2012)
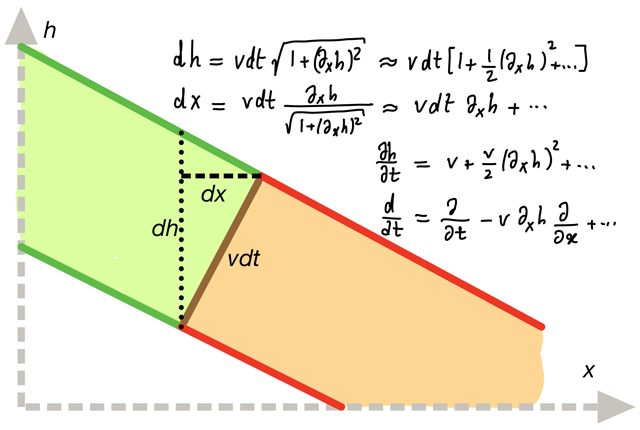
![]() Possible morphologies can be explored by coupling expansion profile (KPZ) and invasion (FKPP) equations (neglecting noise):
Possible morphologies can be explored by coupling expansion profile (KPZ) and invasion (FKPP) equations (neglecting noise):
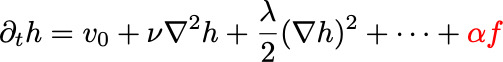
![]()
Uniform (isotropic) growth constrains parameters of the above (gradient expnasion) equations to
A more general class of equations, also including anisotropy, were proposed and studied in connection with extinction transitions, in:
"Bacterial range expansions on a growing front: Roughness, Fixation, and Directed Percolation,"
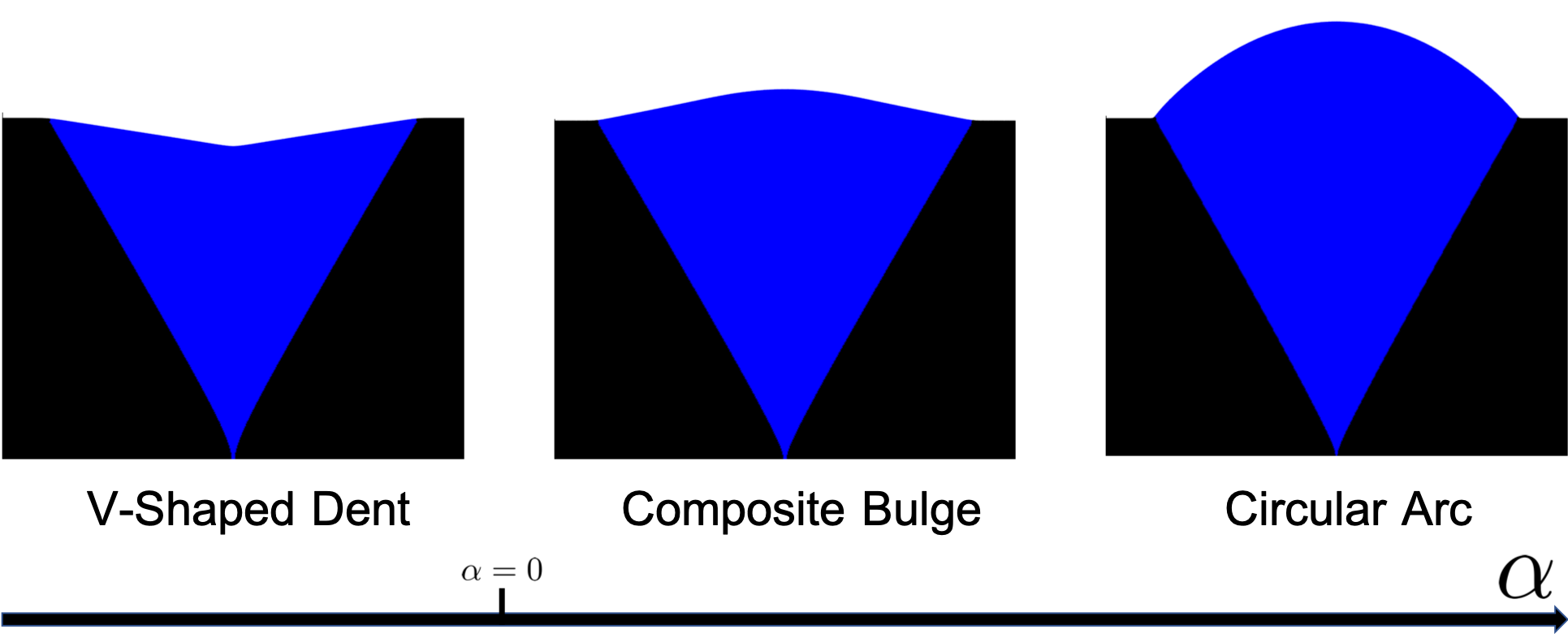
Ignoring invasion front shape, one possible geometry is a Circular Arc:
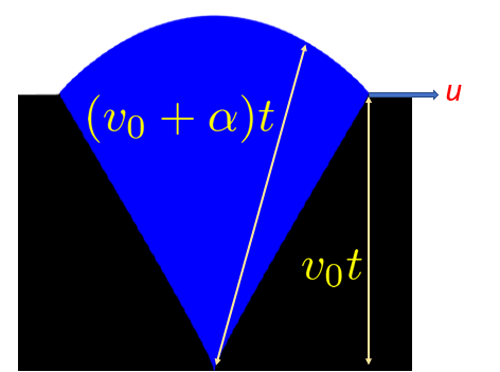
Another morphology is a Composite Bulge joining the flat front at a fixed slope:
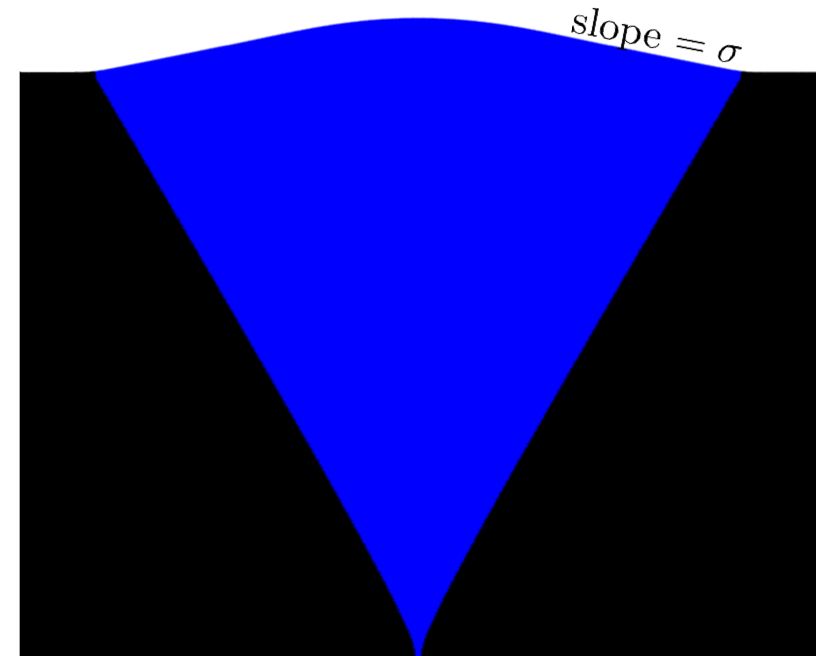
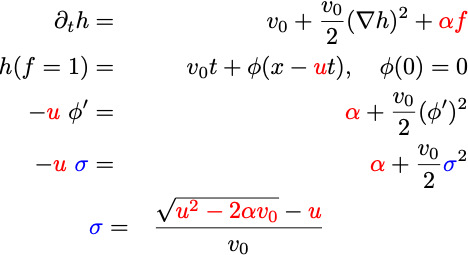
Positive slopes occur for slower mutant growth, leading to V-shaped Dents:
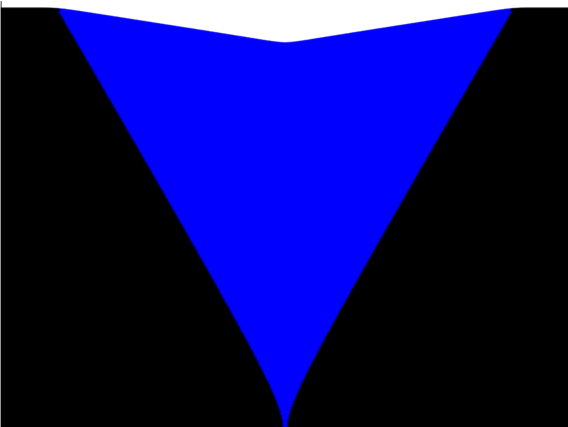


This is somewhat surprising, as slower growth of isolated colonies suggests that they would lose out in competition.
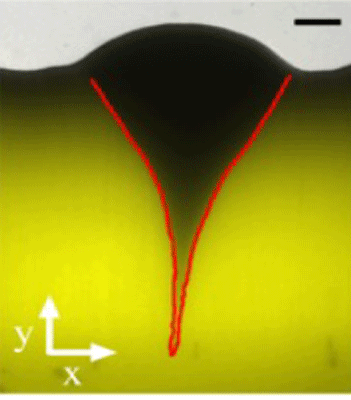
However, such a V-shaped dent, with take-over of a slower growing mutant was observed recently:

"Slow expanders invade by forming dented fronts in microbial colonies,"
Hyunseok Lee, J. Gore1 and K.S. Korolev, PNAS 119, e2108653119.
(Different morphologies obtained through "geometric growth" rules)

![]() Phase diagram of possible growth morphologies:
Phase diagram of possible growth morphologies: