Specialization during Range Expansion

red ball Novel traits  evolve to take better advantage of resources, with concomitant changes in fitness

yellow ball Assume that development of some traits can be indicated by parameter m=b-h ,

such that  m=0  corresponds to the ancester (generalist),          

while   m>0   corresponds to one trait (e.g. height h>b),  m<0    to another (e.g. breadth b>h)      

yellow ball Let us assume for simplicity that the dependence of fitness on  m is expressed as the polynomial

yellow ball The fitter parent in the stepping stone model wins the competition to reproduce

yellow ball The child inherits traits from the parent, but also acquires mutational changes

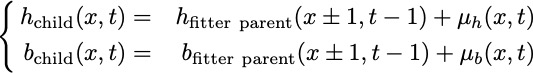
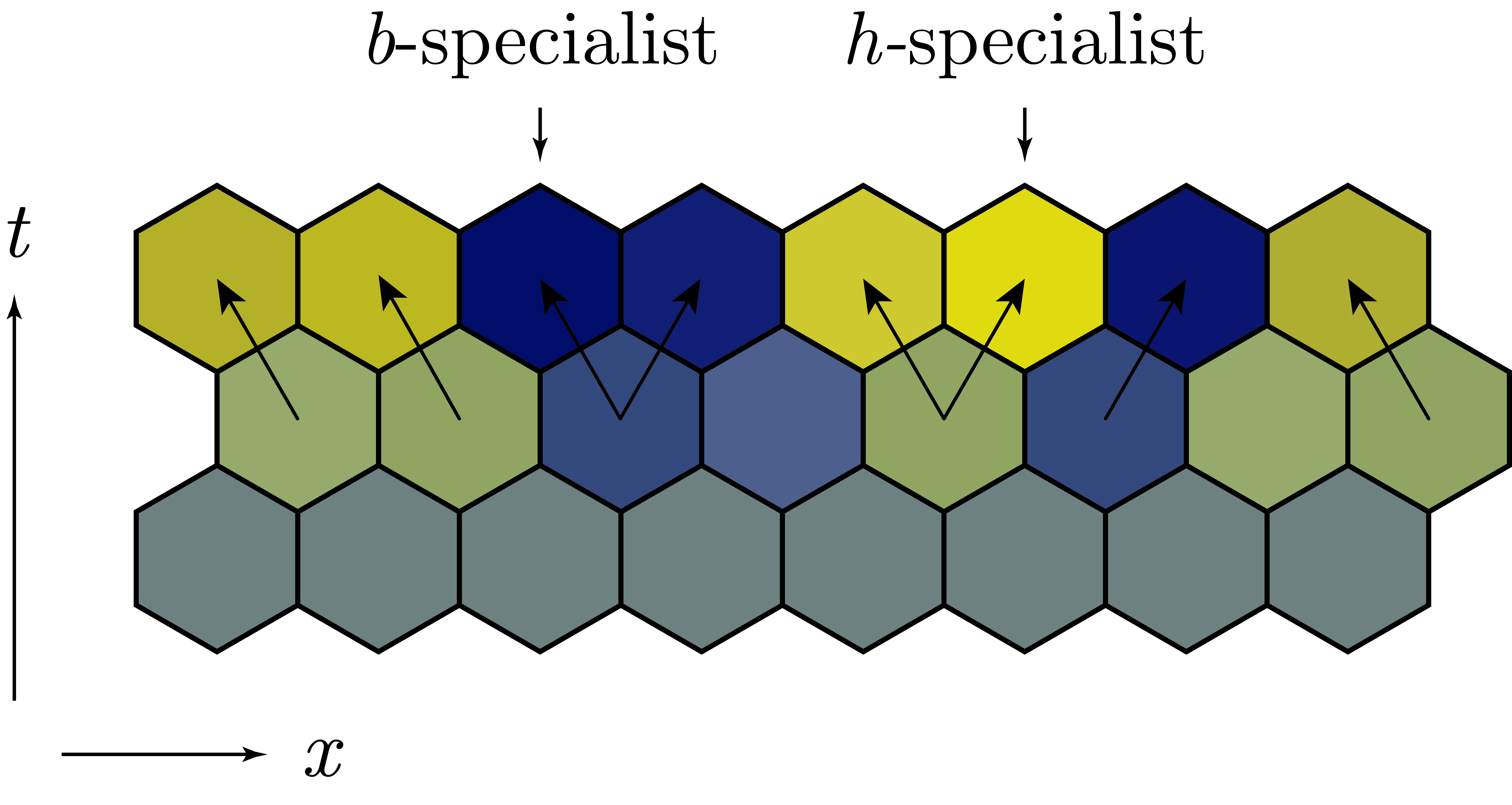
yellow ball Starting with generalists ( m=0 ) at   t=0 , specialists emerge in time through accumulating beneficial mutations:

red ball Distinct growth patterns for different fitness function:

yellow ball 1. Generalists fitness advantage (global)

Peppered moth evolution        

yellow ball 2. Specialists fitness advantage (unbounded)

yellow ball 3. Specialists local fitness disadvantage, but global advantage

yellow ball 4. Specialists fitness advantage (bounded)

red ball Distinct universality classes for bounded and unbounded fitness gain:

  

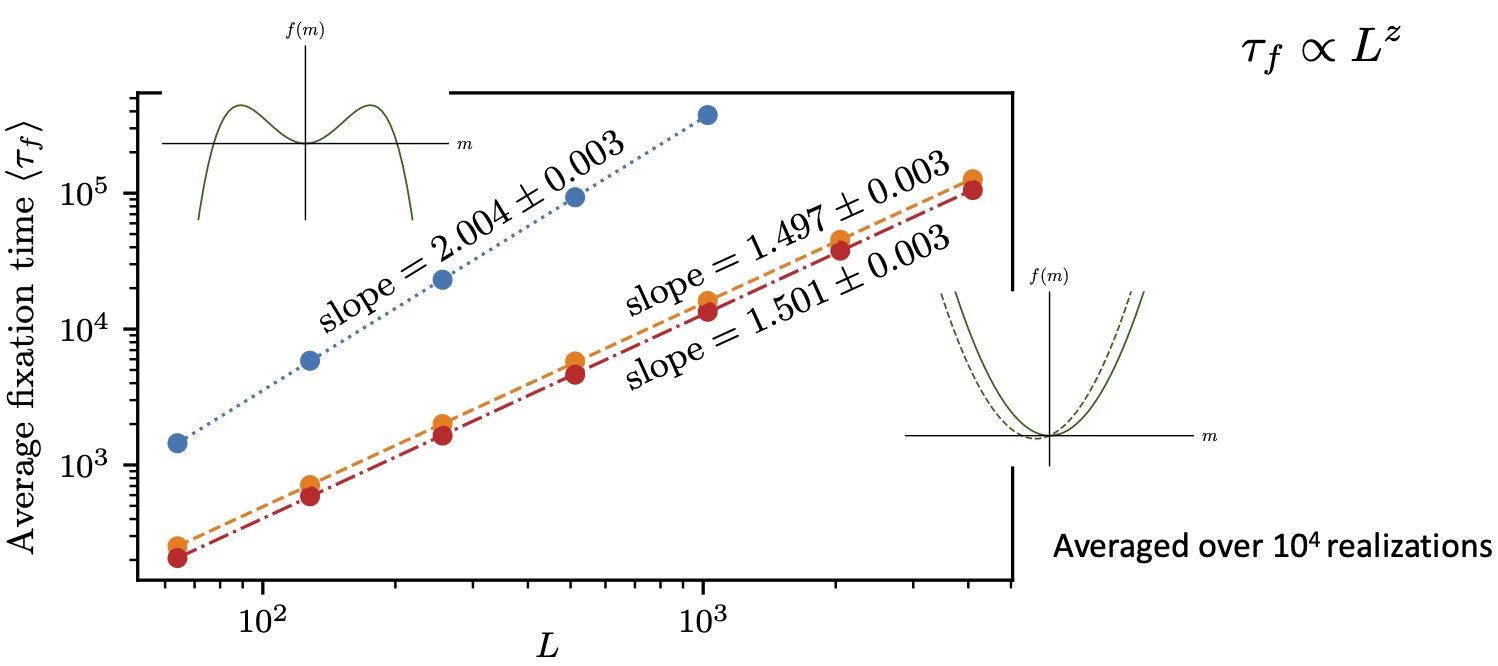
yellow ball "Specializaton at an expanding population,"

Lauren H, Li and M. Kardar, Phys. Rev. E 108, L032402 (2023) (off-line)