Growth Morphology
![]() Beyond their relevance to the extinction transition, the couplings between shape of the front and population reproduction/mutation
Beyond their relevance to the extinction transition, the couplings between shape of the front and population reproduction/mutation
have macroscopic manifestations in morphology of growing films:
The parameter λ indicates the dependence of normal front velocity on slope:
For isotropic growth λ= β1 =vo> 0,
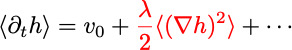
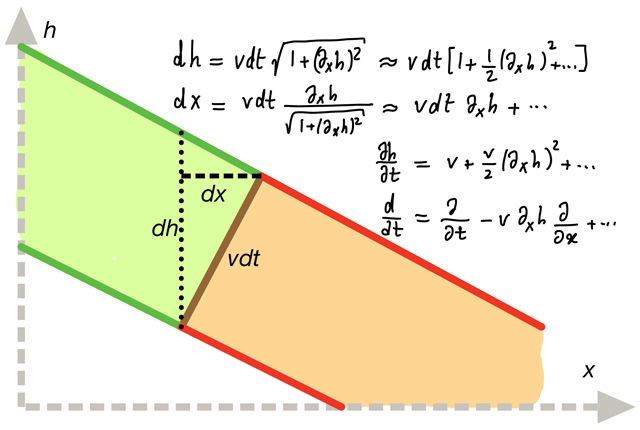
Other growth rules (as in earlier model) lead to λ< 0
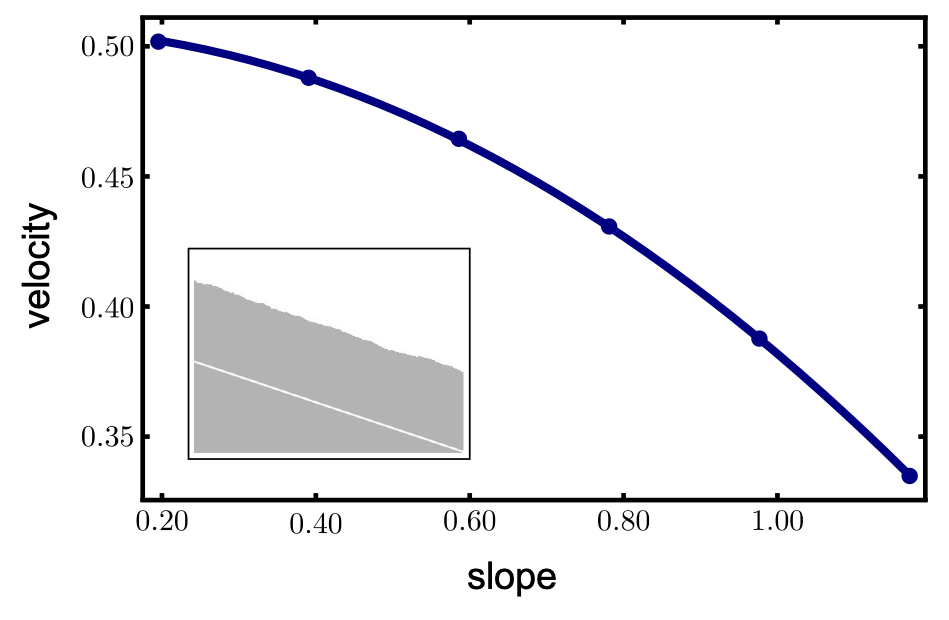
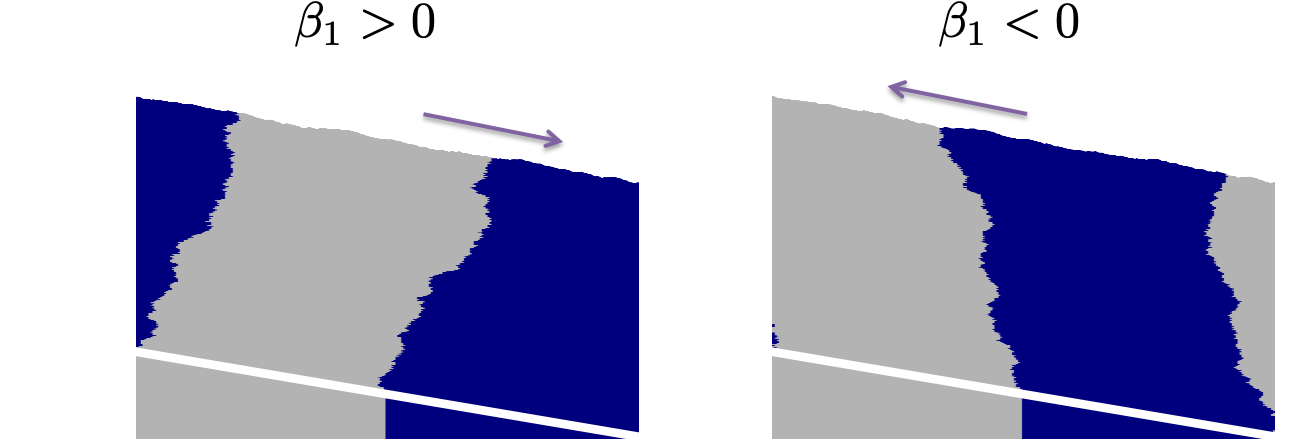
The parameter β1 indicates the in-plane front velocity on slope:

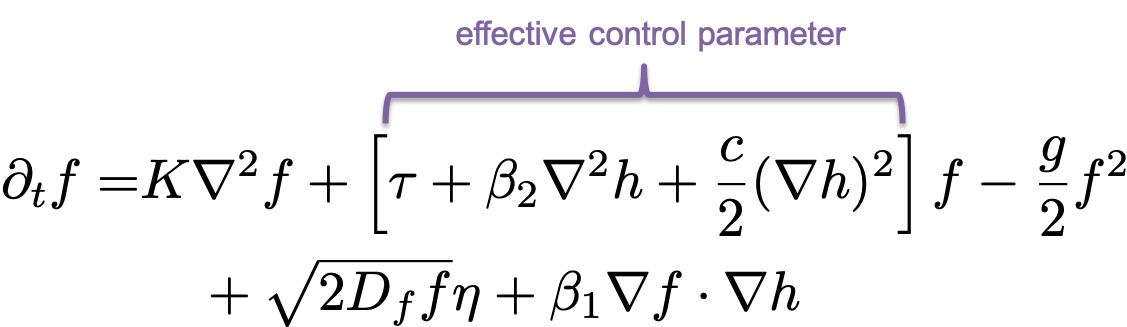
The parameters β2 and c determine the dependence of the extinction point on shape:
![]()
The growth morphology depends chiefly on (the signs of) λ , as well as the growth velocities g and α:
g captures the reproductive fitness advantage; g=0 for netural (non-competitive) fitness
α indicates which species expands more rapidly (normal to the front), e.g. has larger size
Neutral evolution g=0 (equal fitness, no competition) leads to faceted patterns:

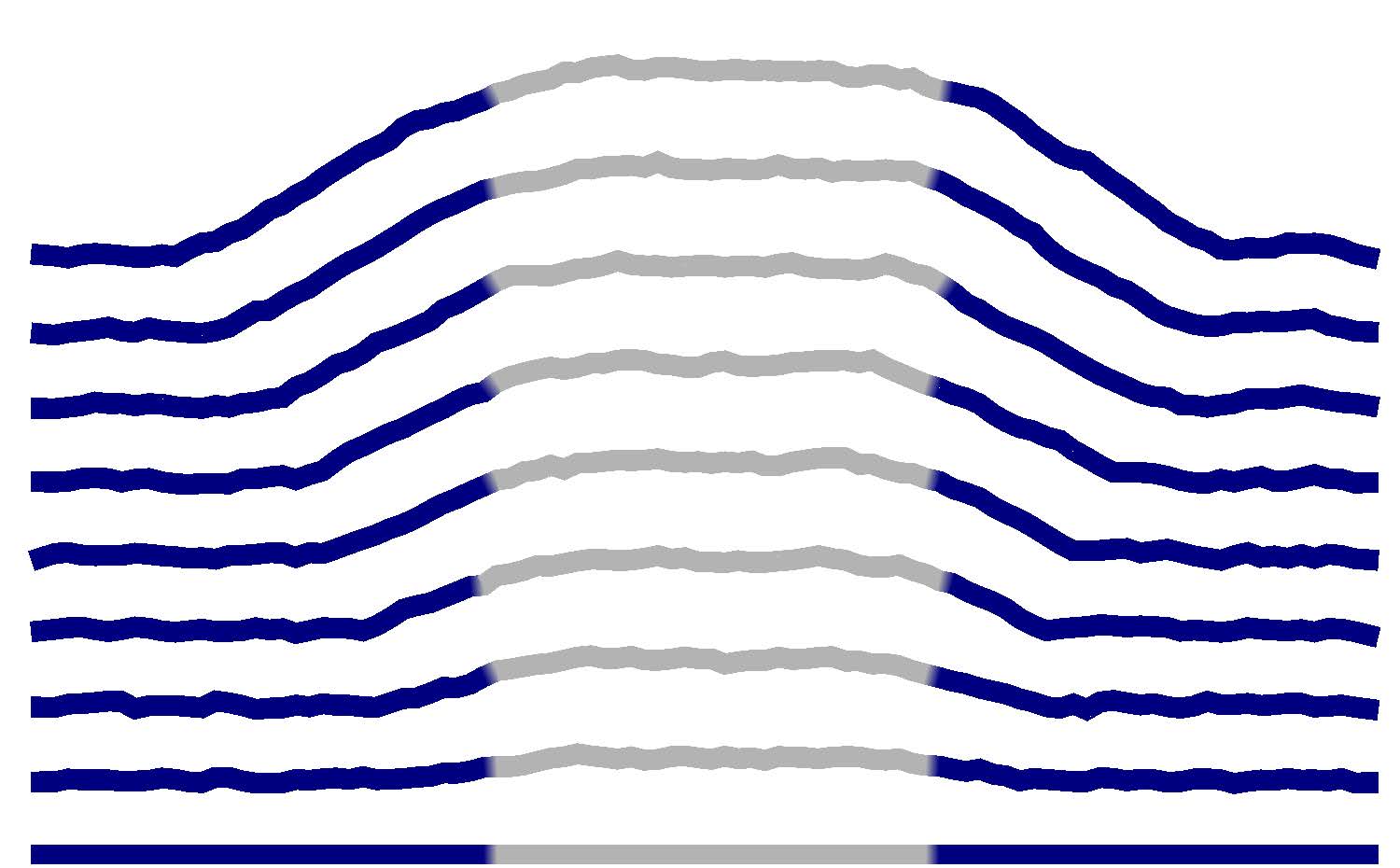
Competitive reproduction (fitter blue reproduces more rapidly) leads to the following patterns:
α < 0 α > 0
 λ< 0
λ< 0 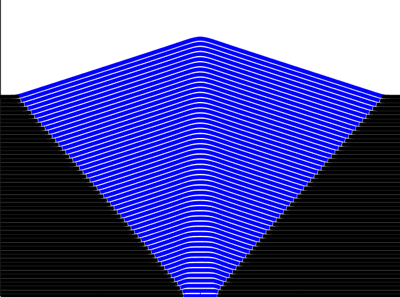
 λ > 0
λ > 0 
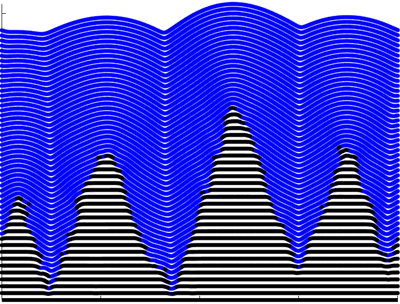
![]() Motivated by experiments on bacterial films, possible patterns for λ> 0 were recently classified in:
Motivated by experiments on bacterial films, possible patterns for λ> 0 were recently classified in:
"Slow expanders invade by forming dented fronts in microbial colonies,"
Hyunseok Lee, J. Gore1 and K.S. Korolev. (2021 preprint)
Observed pattern is an example of competitive growth with λ> 0



Simulations of the stochastic PDEs lead to very similar patterns:
 ==>
==>