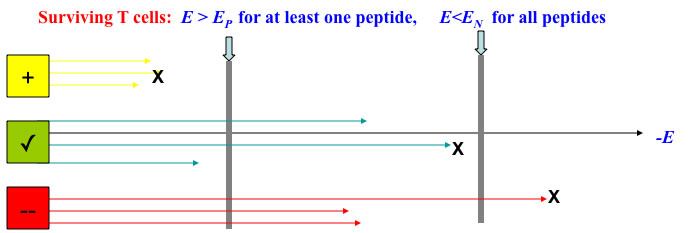
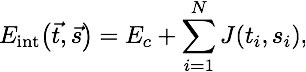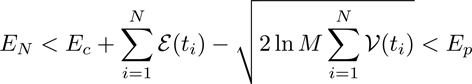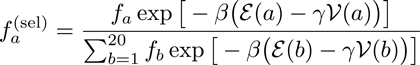Analysis
The selection condition is equivalent to the choice of the Extreme Value:
Probability distribution of the extremum of M objects:
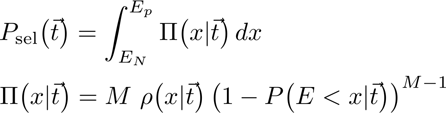
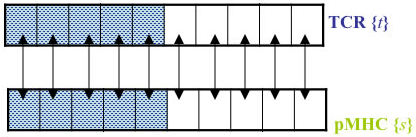
Characteristics of the Extreme Value Distribution .gif)
:
Binding energies of a particular TCR sequencs: 
Extremal mean value: 
~ .gif)
,
where .gif)
and .gif)
are the mean and variance of interactions of the candidateTCR sequence.
Extremal standard deviation: 
~ .gif)
Note scaling in the large N limit; 
(proteome)
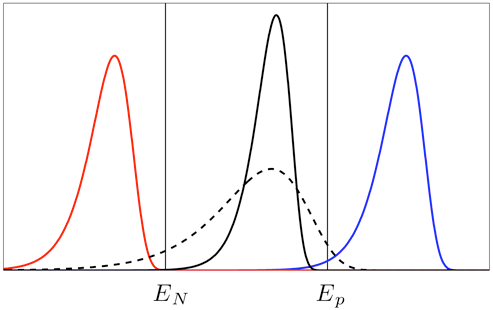
Due to the shaprpness of the distibution in the large N limit, the seletion condition can be written as:
[ and are the mean and variance of interactions of the candidate TCR sequence.]
The above selection condition is reminiscent of the micro-canonical constraints in Statistical Physics.
The "energy" involves interactions amongst the N amino-acids in the sequence 
The "interaction" depends only on the sum of variances for the individual amino-acids
As such, in the large N limit, the probability to select a sequence can be written as a product
,
where 
and 
have to be obtained self-consistently from
and 
.
Graphical solution for
0.gif)
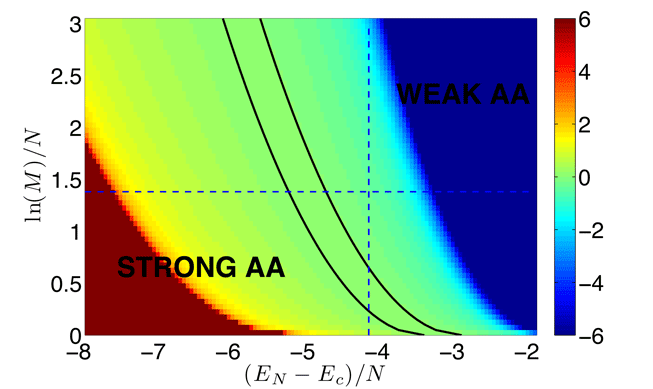
Because of the restriction to an energy interval, there is a range of parameters where = 0.
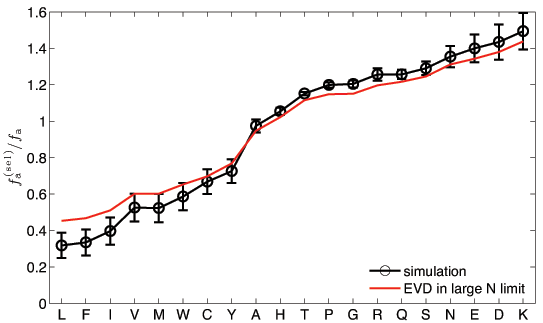
How well does this work for finite N? (N=5 and M=10.000)
A. Kosmrlj, A.K. Chakraborty, M.K., & E. Shakhnovich, PRL 103, 068103 (2009)
More elaborate variants of the above model can be studies (Hanrong Chen), such as
How does non-uniform usage of TCR sites, modify selection bias at different sites?
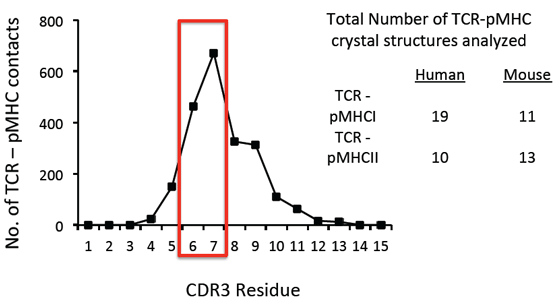
[B.D. Stadinski, ..., A.K. Chakraborty & E. Huseby, Nature Immunology (2006)]
Different sites could be in contact with the same amino-acid peptide. What are subsequent correlations between amino-acids at such sites?