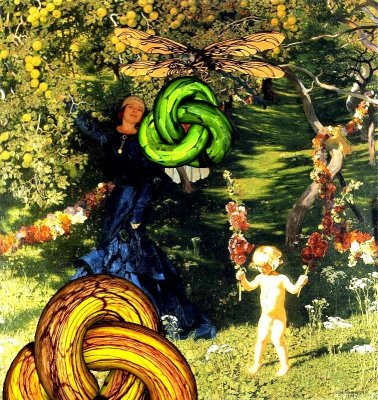Knots in art
by
Piotr Pieranski
Introduction
Scientists tend to think, when a
good idea comes to their mind, that they are the first to have it.
How often they
are wrong!
Not only because
they do not take into consideration that their colleague could have
had a similar idea before.
But also because
they do not at all take into account the possibility that
an ordinary
man could be the first, many, many years ago.
Ordinary people
do not publish, but, fortunately, what they do is of interest for
artists.
Artists record
the life and work of ordinary people.
This happens quite
often, in particular when the ordinary man happens to be a beautiful,
young girl.
I am searching
the archives for convincing evidence of my claim, and I think I
have already found some.
It is the aim of
the essay to present results of my search. It is up to you to decide,
if I'm right.
Obviously, I focused
my attention on the science of knots.
This is more
or less the content of Part I.
Having it ready I discovered that there is a lot of other information
gathered as a side product of my main research.
Thus I decided to extend the work and step by steps six more parts
were born.
Part II deals with the vital question if
looking for the ideal knot, thus, first of all, untangling the knots
is safe and easy.
Part III is just a warning what a wrong
approach to the untangling activity can do to a man.
In Part IV I am trying to present the beauty
of knots, in particular those, in their ideal conformations.
Part V tries to answer the touchy question
where from the mathematicians take their brilliant ideas.
Part VI presents my discoveries concerning
the very beginnings of the knot theory.
In Part VII I present some chilling or
funny stories from the history of the knot theory.
I put a lot of effort to illustrate well my discoveries.
Fortunately, as you will see, prophetic Polish painters provided
me with a lot of a ready for use materials.
Final remarks, acknowledgments and excuses
<---- are here
Who was the father of the ideal knot problem?
As I have discovered, we should rather ask "Who was
the mother of the ideal knot problem?"
Why? After an extensive study,
I come to the conclusion,
that the first person to
think of the knot tightening problem
could have been a young female
Polish shepherd met by Jozef Chelmonski.
Have a look at the picture below.
The gossamer knot is hardly visible, but it is there!

Gossamer with a knot
(based on Gossamer
by Jozef
Chelmonski)
A similar problem, although in rather different circumstances,
was also considered by an anonymous
lady known by Wojciech Gerson,
a Polish painter living at the
end of the IXX century.
Her quite original idea was to
use the viscous drag of the flowing water
to tighten and untangle knots.
The Rest with the Entangled Trefoil
(based on The
Rest by Wojciech
Gerson)
As it often happens, the same ideas were born, independently,
in many minds.
There exists a convincing evidence, that also a lady
known by Amadeo Modigliani was
making some experiments with untangling
knots. Her position in the knot tightening debate
was, apparently, completely different.
Reclining
nude untangling a knot
(based on: Reclining
Nude from the Back by Amadeo
Modigliani)
One of the most intriguing questions that every mathematician
asks him/her-self in his/her childhood is:
Where do the ideal knots come from?
Well. The question is touchy in the case of humans. You know: awkward facts
of life.
Fortunately, in the case of knots the situation is simple and clear.
One of the pictures by Chełomoński is devoted to it.
It shows Jun O. making his first scientific discovery:
Theorem I.1. Ideal knots are delivered by storks.
Seeing is believing. No proof is needed.
New arrival
(based on Storks
by Jozef
Chelmonski)
Is bringing a knot to its ideal conformation safe and easy?
As we know, tightening a knot may bring it to the
ideal conformation. It was probably
very late evening, that a girl
observed discretely by Georges de La Tour managed to
tighten a quite complex achiral
knot to its ideal conformation.
She seems to be satisfied with
her work.
It took her not more than a while
to arrive at the final conformation.
(Have a look at the oil lamp. Only
a bit of the oil is missing.) )
Magdalen with a knot
(based on: Magdalen
with the Smoking Flame by Georges
de La Tour)
Needless to say, not all endeavors
to untangle knots and bring them to the ideal conformations
are successful.
The knot untangling business is not a joke. Look at the poor boy
portrayed by Caravaggio.
Being bitten by an entangled knot is not a pleasant experience!
Boy bitten by a knot
(based on: Boy
bitten by a lizard by Caravaggio)
One of the most spectacular failures
was recorded by the Norwegian painter Edvard Munch.
He spent a part
of his life in Paris and Berlin. It could be in Berlin, I guess, that
the tragedy
depicted in one
of his most famous pictures took place. The fellow shown on the left
failed completely.
That is why he
is hiding his face. The lady has had already her first try.
Apparently: unsuccessful.
She is depressed but not hopeless.
Which was the end
of the knot untangling party?
Gloomy, I guess.
Tangle
(based on: Ashes
by Edvard
Munch )
Problems of the Norwegian couple
are not strange to me.
The particularly
nasty knot they recklessly decided to play with has a bad reputation.
You will find it
in one of the most famous Polish pictures by Jan Matejko.
It shows the royal
joker, Stanczyk, thinking about the problems of Poland.
To be more precise:
thinking about the relation of Poland with its neighbors.
The relation is
the famous Polish Gordian Knot.
Stanczyk thinks about the Polish
Gordian Knot
(based on: Sta?czyk
w czasie balu na dworze królowej Bony wobec straconego Smole?ska,
Jan
Matejko)
What is a depressing problem to some people, can
be a source of joy to others.
It's just the matter of an appropriate
approach to difficulties.
A splendid illustration of this
truth can be found in paintings of Axentowicz.
Have a look at the young lady portrayed
by the gifted Polish artist.
Being young and beautiful, the
lady does not get depressed when she finds the Polish Gordian Knot
too difficult to untangle.
She treats the sinister knot as
an intriguing piece of jewelry. How charming is she checking if it
matches her carnation.
Don't you agree?
(I think, I'm slightly in love
with the girl. And I feel she likes my knot. The power of art is
incredible. Just try.)
Spring looking at a knotted jewel.
(based on Spring
by Teodor
Axentowicz)
What a wrong approach to ideal knots can do to a man.
Contemporary artists are also interested
in the ideal knots problem.
Obviously, their
view is completely different. It is so, because the world around
them is different:
more aggressive,
dangerous, terrifying. People involved in the knot untangling business
are often perverted.
A good example
of what a wrong approach to the untangling activity may do to a
man has been
illustrated by
Starowieyski. His "Serial knot untangler" shows a monster
ready to use his
brutal skill on
a completely helpless knot. To me it is awesome.
Certainly, not
all means leading to the ideal goal are permitted.
Serial knot untangler
(based on: Nieuchwytny
morderca by Franciszek
Starowieyski)
That untangling knot can be connected
with perversion was known already to ancient Greeks.
As I have found
out, the activity for which Oedipus gained such a terrible reputation
was but a cover
to something even
more terrifying. Not only he was untangling knots by himself using
non-Reidemeister moves,
but he also
was ordering it to his own son! Henry Fuseli revealed this horrifying
truth.
Just look at the
poor juvenile. How hideous this order must have been to him.
Non-Reidemeister
moves! Gosh!
Oedipus ordering his son to use
non-Reidemeister moves
(based on: Oedipus
Cursing his Son, Polyneices, Henry
Fuseli)
Entangled knots are not good for human minds.
Among the artists who knew this
simple truth was Edgar Degas.
He seems to be the first to discover
the cause of the blue mood ubiquitous among the absinth
drinkers:
nastily entangled, knotted molecules
of higher cyclic alcohols.
Today we know: mind is not able
to untangle them.
On the contrary, the naughty molecules
easily entangle the mind.
(Try. With caution!)
Knots drinker
(based on : Absinth
drinker by Edgar Degas)
The beauty of ideal knots
Let me change the mood.
From the gloomy
one to more optimistic.
Untangling knots
is neither easy nor safe, but the result - ideal knots - are worth
the risk: they are pretty!
Some artists knew
this before the scientists started to think about them.
There are many
wonderful examples of ideal knots depicted in the most precious
pieces of art.
Being Polish, I
went through the art galleries trying to find ideal knots in pictures
painted
by Polish artists,
in particular those, whom I like most: Wyspianski, Axentowicz, Zmurko.
I think I have
found some interesting pieces.
Let me start with
Zmurko. He is less known, but as I find, his knowledge of ideal knots
was deep.
One of his paintings
can be seen as a proof of the existence of ideal knots. I like the
proof.
In contrast to
the proof by Cantarella, Kusner and Sullivan, Zmurko's proof is
full of warmth and feelings.
(CKS, sorry, but
this is true.)
A cigarette, a fan and an ideal
trefoil
(based on: A
fan and a cigarette by Franciszek
Zmurko)
It seems that many Polish artists who spent some
time in Paris were aware of the existence of ideal knots.
Certainly, Wyspianski knew they
existed. More. He was apparently aware that the path leading to the
ideal
conformation could be blocked by
the misleadingly beautiful, local minima.
Looking at his Girl with a knot
you will certainly recognize the Gordian Unknot.
Neither I, nor anybody else was
able to provide a formal proof of its existence.
Wyspianski's approach is different:
"The proof of the pudding is in eating".
He simply portrayed it.
Girl with the Gordian Unknot
(based on: Girl
with a flowerpot by Stanislaw
Wyspianski)
As we are with Wyspianski, my favorite
painter, let me tell you something more about him.
His intuitive knowledge
of the knot theory must have been a good one.
In one of his paintings,
we find a clear image of a nicely tightened, big achiral knot.
Girl with an achiral knot
(based on: Girl
in a hat by Stanislaw Wyspianski)
In another, I recognize a toy in form of a cable knot.
Sleeping Mietek with a cable knot
(based on: Sleeping
Mietek by Stanislaw Wyspianski)
To end with something special, let
me introduce to you another remarkable Polish painter, Jozef Mehoffer.
In Friburg, Switzerland,
you may find his wonderful stained glass pictures. Here, I would
like to make you
acquainted with
one of the most unusual piece of his work, a dream-like picture of
a garden.
It would be strange,
if there were no ideal knots in it. There are two, both trefoils.
Strange garden with trefoil knots
(based on: Strange
garden by Jozef
Mehoffer)
Where does the inspiration of the knot theorists come from?
The number of scientists involved in studies connected
with the theory of knots grows at an exponential rate.
Why? From where do they take their
most brilliant ideas?
These are the questions which I
am asking myself quite often, in particular when I am reading
papers written by my mathematically
oriented colleagues.
Due to the apparent time worm-holes
Polish painters were able to provide answers to the questions
before the questions have been
posed.
One of the less known Zmurko's
paintings reveals the truth. The pleasant truth, I would say.
(More and more I am tending to
think that maybe I should have become a mathematician, not a physicist.)
Inspiration of Eric R.
(based on Widzenie
Fausta by Franciszek
Zmurko)
The method used by Eric R. reminds me "Joseph Balsamo",
the novel by Alexandre Dumas (father),
which I was secretly reading in
my youth.
That mathematicians are able to
convince brilliant girls to share their secret thoughts with them
is wildly known.
Another story of this kind has
been recorded by Axentowicz..
The victim is different, the predator
is different, the method is different.
but the goal the same - a brilliant
idea.
Inspiration of Rob K.
(based on Reading
girl by Teodor
Axentowicz)
Some scientist are too shy to do, what Eric R. or
Rob K. do, to find brilliant ideas.
It does not mean, of course, that
their minds are free from temptations.
And temptation, as we all know,
can be easily transformed into reptation.
Once more it has been Axentowicz
to reveal the truth.
Temptation of Tetsuo D.
(based on Redhead
by Teodor
Axentowicz)
Not always the circumstances at which mathematicians
get their best ideas are so dramatic.
Sometimes, the ideas appear all af a sudden when nobody
really expects them, e.g. during a picnic.
It was a sunny Sunday afternoon. (I cannot find out at which AMS spring meeting it was.)
Jon S. and Greg B. were enjoying an afternoon tea, when
a very good idea came to their mind.
They left for a while the company to discuss it in private..
This very moment has been recorded by Gierymski.
The subject of the discussion will remain unknown. Peccato!

Jon S. and Greg B. discussing a new idea
(based on W altanie by
Aleksander
Gierymski)
Good ideas can be fished for also in tranquility,
far from the hectic life of modern society.
I find an example of this approach in one of the paintings
by Siemiradzki.
He shows Ben L. after two days in raw spent at the keyboard.
Ben seems to be innocently watching the fishing children,
but it is only appearances, appearances...
Can you see the ideal knot resting behind the tree? In a
while Ben will grab it.
I know he will. Have a look at his home pages. The poor
knot is there!

Ben L. fishing for ideal knots
(based on Fishing by Artur
Siemiradzki)
The true origin of the knot theory
Knot theory, as a part of topology is dated for a
bit more than 200 years.
Is this right?
My visit to Las Vegas convinced
me that this dating may be completely, absolutely, totally wrong!
Why?
Just have a look by yourself at
the picture I took at the entrance to one of the biggest casinos.
Don't you think the sphinx could
have been a knot theorist?
I think he was.
The first knot theorist
(based on the photograph
taken by the author)
Knot theory was born in sweat and pain.
The birth of the physics of
knots took place in radically different circumstances.
That this was the case one can
see looking at another painting by Axentowicz.
No sweat. No pain. Just a friendly
look.
And a knot of a mutual understanding.
Maybe more.
The birth of the physics of knots
(based on Redhead
by Teodor
Axentowicz)
Knot X Files
Stories from the history of knot theory
Which is the use of the
knot theory?
I'm very often asked the question.
(By people, who are not able to tie properly their shoelaces.
I happen to know some. They claim that finding an ideal
knot is a problem of logistics.)
Gosh! Have a look at historical paintings by Grottger.
There you will find the answer,
Let me explain. Polish national sport is plotting
uprisings.
It is important, since it is only due to the sport that we
managed to survive as a nation.
To win an uprising you need weapons.
The picture, to which I am drawing
your attention, shows Polish mathematicians preparing lethal knots.
You may recognize the face of one
of the fellows who hammer the knot.
Yes. It is our Canadian ally, Rob S.. the famous knot
plotter.
(Thanks Rob! Great job! It's not your fault that the
uprising was lost.)
Rob S. hammering a knot
(based on Hammering scythes by Artur
Grottger)
Strange enough, most applications
of the knot theory are connected with rather violent events.
To support my claim let me present another historical masterpiece
by Matejko.
This time he reconstructed a really gloomy story.
One of our best queens, Bona, was poisoned. She had lots
of enemies. It was her to introduce la verdurra into our traditional
kitchen.
As the legend says, the royal knot theorist, Jon S. was trying
to save her life with the extraction from an ideal knot.
(Click on the image to see it better.)
And what?...I am sorry to say - it did not work.
I think he used too simple knot. He used a trefoil. Perko claims 10.161 or 10.162 would be better.
The royal knot theorist trying to
save Queen Bona
(based
on Poisoning of Queen Bona by Jan
Matejko)
Question "Why does the trefoil knot weaken ropes
more than the figure eight knot?" bothered human race for centuries.
Some people lost their lives trying to find the cause of this
crucial law of nature.
In vain. The puzzle remained unsolved.
It needed the brilliance of Giovanni D., his Italian
fantasy, to arrange a proper experiment and find out the truth.
Once more let us visit the gallery of Matejko's work.
The picture below shows Giovanni D. at the moment of the discovery.
Notice the bunch of spaghetti at his feet. Crucial experiments
were done before.
What you see is but the moment of illumination: CURVATURE!
Yes! CURVATURE!

Giovanni D. discovers the truth
(based on: Copernicus or the dialog with the God by Jan Matejko)
Matejko, Matejko... Not too much of the Matejko? NO!
He deserves it. It were his paintings that stimulated our imagination where we were children.
Stories told by Matejko's brush get deep into the memory of every Polish child.
For instance, the story of the alchemist Greg B. vel Sedziwoj.
He was an alchemist. But he was different from other alchemists.
They were looking for the philosophical stone. He was looking for the philosophical knot.
He succeeded. The picture shows Sedziwoj showing the philosophical knot to the King Sigmund III.
(I think, it's 4.1. Ideal conformation.)

. Sedziwoj presenting the philosophical knot to King Sigmund III
(based on Sedziwoj by Jan Matejko)
It would be an unforgivable mistake, if you were not introduced to the art of Jacek Malczewski.
His painting is highly symbolic. Things and events you see in his pictures have hidden meanings.
Looking recently at one of the pictures I realized how prophetic Malczewski was.
The mysterious Coronation of the Swiss King of Knots now reveals its sense.
I think I recognize the face of the king. Yes. No doubt. It's Andrzej S.
He accepts the crown with dignity and modesty.
One cannot oppose the will of gods.
Amen.