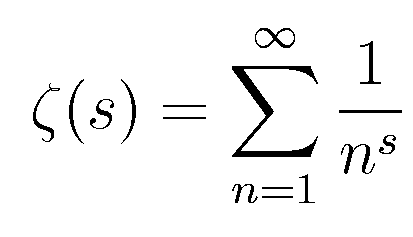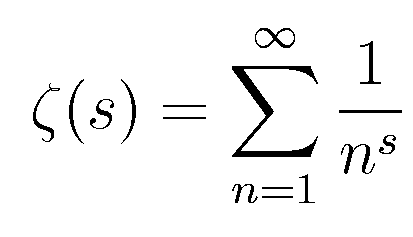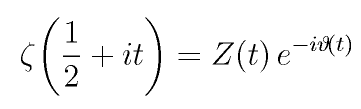Tabulating values of the Riemann-Siegel Z function along the critical line

or

Creating a 14 hour sound file with a supercomputer

Ken Takusagawa

Zeta function

Riemann zeta function
$\zeta(s)=\sum_{n=1}^{\infty}\frac{1}{s^n}$
The Riemann conjecture states that all non-trivial zeros of the zeta function occur along the line Re(s) = 0.5. This line is known as the critical line.

Zeta function

plot of zeta

Z function

The Riemann-Siegel Z function is a real-valued "precursor" to the Zeta function along the critical line.
See Glen Pugh's Z(t) plotter . Try t= 15457423.7117588
It looks like an sound wave!

Riemann-Siegel formula

The Riemann-Siegel formula takes O(t^1/2) operations per point.
I checked the derivation of the formula.
Hurrah! No typographical or arithmetic or simple algebraic errors.
C₆ = 1/563585608581120/pi^12*P18 + 18889/237817036800/pi^8*P10 + 17/652298158080/pi^10*P14 + 367/7864320/pi^6*P6 + 5/2048/pi^4*P2

Parallelization

Deal out chunks of the domain to each processor.
One domain: Starts at t=0, roughly 100 hrs computation, 800 MB losslessly compressed.
Another domain: Starts at t=2.6e+11, 35hrs computation, 1.7MB.
And they sound like.. .

Spacings of the zeros

distribution of zeros

Fourier transform

power spectrum

Conclusion: Listening to the thing

14.8 hours, or 0.618 day (golden ratio)
Masked by computer noise