Ground-based interferometers (IFOs) have serious limitations that cannot be overcome. Even with the facilities working at their most sensitive, gravitational waves (gw) of frequencies below 10Hz simply cannot be detected. Sensitivity is limited by seismic (geophysical and man-made) noise.
This means that many gw from interesting sources (such as massive black holes) cannot be detected.
The diagrams below show the noise curves for LIGO. As you can see, even at its most advanced it isn't detecting the low frequencies and is mainly restricted by seismic noise.
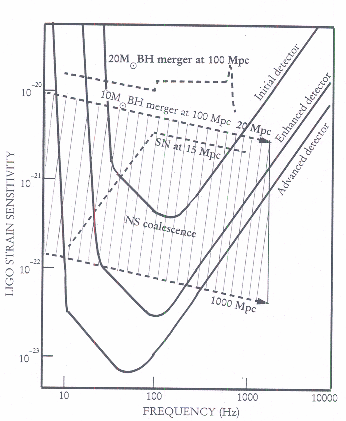
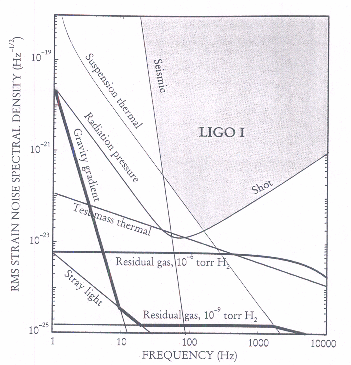
To remove this limit on sensitivity at low frequencies, we can take the IFO away from the seismic noise--send it into space. This is a huge project. If it is approved, it will start being built in 2004 with a launch in 2011.
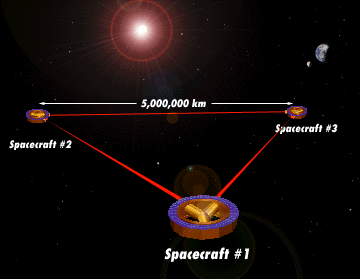
The idea is to have three spacecraft flying in an equilateral triangle formation. The length of the triangle side will be five million kilometers.
GWs will stretch or contract the space between the spacecraft. These changes in distance will be detected using laser interferometry, just like the ground-based IFOs but the interferometer arm length is a million times longer and so a million times more sensitive. Plus it is not affected by seismic noise.
This is a problem in space that does not exist in ground-based IFOs--how to keep the distance between the spacecraft constant. Even changes of a micrometer in a length five million kilometers long is a problem.
One thing that could change position is variation in sunlight. This would force the spacecraft to move because photons exert a force due to the fact that they have momentum (from the relation E = pc). The solution to this is to contain the "proof masses" within the spacecraft and to shield them from sunlight. The distance measured by interferometry is the distance between the proof masses, not between the spacecraft. The position of the proof mass in relation to the spacecraft will also be measured and if changes are detected, thrusters will correct for it and move the spacecraft back into position.
[Aside: Controlling the position of the spacecraft in this way is common and used to correct the positions of low Earth orbiting satellites slowed due to friction or drag with the atmosphere. Hence this operation is called "drag-free" operation.]
The position of the proof mass relative to the spacecraft is important because even the spacecraft exerts a gravitational pull on the masses. A variation of spacecraft-caused pull on the masses will affect results and so the drag-free operation is necessary. Since the pull is not great, the relative distance does not have to be kept constant to the same degree of accuracy as the distance between the proof masses.
Even more likely to change the positions is the gravitational pull of the Earth. Therefore, LISA needs to be as far away from the Earth as possible. Unfortunately, cost is also an issue in the real world and the amount of propellant needed to get the spacecraft far from the Earth is too high to be justified. The proposal is to have LISA centered 20 degrees behind the Earth, which is a good compromise between cost and sensitivity. It is also a benefit for telecommunications--having LISA far away would increase the time it takes for signals to be sent and received.
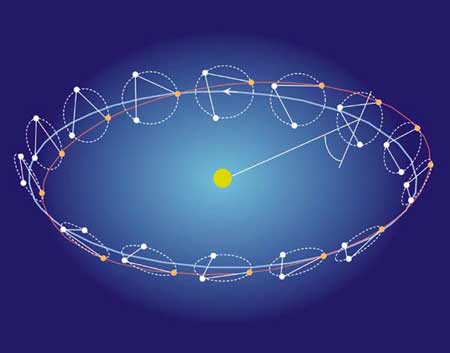
The distance between the spacecraft must remain the same and the orientation of the triangle must change to determine the direction of the gws.
With those restrictions in mind, the orbit of LISA will be Earth-like. It will have a period of one year and go around the Sun. The planes of orbit will be slightly elliptical and tilted such that the triangle formation is kept but the orientation changes.
As the configuration of LISA changes with time, this puts a limit on the lowest frequency (longest time period) gw that can be detected.
Amplitude and phase changes from the gw source over the course of the year will determine the direction of the source.