Figure 2
I have to admit that I am finding some pleasure, for entirely disreputable reasons, in the weakness of the new European currency. In fact, I'm in "Hershey heaven".
The term comes from Horace Freeland Judson's book The Eighth Day of Creation, about the emergence of modern biochemistry. Alfred Hershey was a noted experimenter who once described his vision of scientific happiness as "Having an experiment that works, and getting to do it over and over again." Any scholar knows the feeling: there is no joy quite like that of research gone well, and in a perfect world you would be able to recapture that joy reliably - preferably by finding that your greatest professional hits can be recycled endlessly.
Now my most successful single paper was surely "Target zones and exchange rate dynamics", published in the Quarterly Journal of Economics in 1991 (though a draft was widely circulated back in 1988). (The paper is in my collection Currencies and crises ). It was (duh) about target zones - official ranges for exchange rates - and how they affected market behavior. And it was indisputably nifty.
Of course, the euro isn't in any official target range. But it is clear that having introduced it at a value slightly more than a dollar, European officials are reluctant to see it drop below parity. They shouldn't try to support the euro on economic grounds, and they might not; but then again they might. And so the new euro offers a classic example of an imperfectly credible, one-sided target zone.
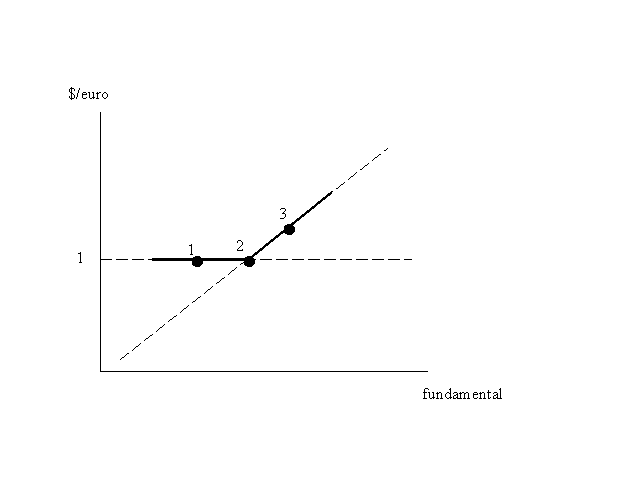
The analytical idea of my old paper was to think of the current exchange rate as determined by two things: some "fundamental" value - what the exchange rate would be if it were not expected to change - and its own expected rate of change. And for simplicity the fundamental was assumed to follow a random walk. So absent any target zone the exchange rate would simply be equal to the fundamental; in terms of Figure 1 , the exchange rate would slide up and down a 45-degree line.
Suppose, however, that the ECB attaches - or is believed to attach - some special significance to an exchange rate of 1. (After all, if the euro drops below that level, it will be worth less than the Argentine peso!) A naive view would be that the actual relationship between the euro and its fundamental determinants would look like the solid line in the figure: as long as the euro is safely above $1.00, it will be equal to its fundamental value, but the ECB will do something to prevent it from falling below. But if market participants are sophisticated, matters will not be that simple. The reason is illustrated by considering what would happen if the current level of the fundamentals were at point 2, putting the euro just above $1. If the fundamentals were to improve a bit, the euro would move to 3 - appreciating significantly. If they were to worsen, however, the euro would move only to 1 - hardly any depreciation. So even though the fundamental is as likely to fall as rise, the exchange rate would be on average expected to rise; and this expected appreciation would itself drag the exchange rate above the fundamental.
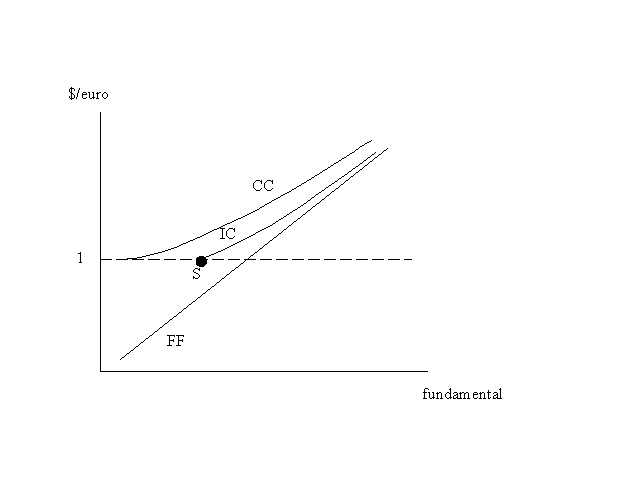
Following the logic through (and, if you want to do it right, doing the stochastic calculus), you find that a completely credible commitment to keep the euro worth at least $1 would imply a relationship between fundamentals and actual exchange rate that looks like the curve CC in Figure 2 . It turns out that this curve must be just tangent to the horizontal line at the parity 1 - the celebrated (among people who do this sort of thing) "smooth pasting" condition. But the main point is that the expectation that the ECB will do something to support the euro at $1 keeps it above its fundamental value even when it is some distance above the support level.
Now factor in the fact that while the ECB might intervene to support the euro, then again it might not - and there is no way to know until Mr. Duisenberg is actually put to the test. What must happen then is that until the uncertainty is resolved, the relationship between the euro and its fundamental will be like IC, somewhere intermediate between the "completely credible" curve CC and the "free float" line FF. (Where depends on the probability the market attaches to the ECB doing what is necessary to keep the euro above $1). And the rate will randomly walk up and down IC.
If the ECB is lucky, this random walk will never take it to the sticking point. But if the random walk should take the euro down to point S, a very awkward situation will result. If the ECB does the wrong thing, and does something (raising interest rates in a sluggish economy?) to support the euro, the value will jump to the CC curve. But if it does not - if, in other words, it acts sensibly - then the markets will know that it's a free float after all, and the euro will drop sharply. This will do the European economy no harm, but will be highly embarrassing to European officials.
Of course, all of this is silly. If the euro had been constructed so
that its starting value were $1.50, or $0.75, there would be no line in
the sand, and what is really a minor fluctuation (remember that the dollar
has oscillated between 80 and 150 yen over the past 5 years) would not
be causing so much anguish. On the other hand, the whole EMU project is
arguably a triumph of symbol over substance; so there is poetic justice
in seeing its leaders in trouble because a symbolic line of no substantive
importance may soon be crossed. Anyway, I personally am having fun.