JAPAN'S TRAP
Paul Krugman
May 1998
Japan's economic malaise is first and foremost a problem for Japan itself. But it also poses problems for others: for troubled Asian economies desperately in need of a locomotive, for Western advocates of free trade whose job is made more difficult by Japanese trade surpluses. Last and surely least - but not negligibly - Japan poses a problem for economists, because this sort of thing isn't supposed to happen. Like most macroeconomists who sometimes step outside the ivory tower, I believe that actual business cycles aren't always real business cycles, that some (most) recessions happen because of a shortfall in aggregate demand. I and most others have tended to assume that such shortfalls can be cured simply by printing more money. Yet Japan now has near-zero short-term interest rates, and the Bank of Japan has lately been expanding its balance sheet at the rate of about 50% per annum - and the economy is still slumping. What's going on?
There have, of course, been many attempts to explain how Japan has found itself in this depressed and depressing situation, and the government of Japan has been given a lot of free advice on what to do about it. (A useful summary of the discussion may be found in a set of notes by Nouriel Roubini . An essay by John Makin seems to be heading for the same conclusion as this paper, but sheers off at the last minute). The great majority of these explanations and recommendations, however, are based on loose analysis at best, purely implicit theorizing at worst. Japan is depressed, we are told, because of too much corporate debt, or the refusal of banks to face up to their losses, or the overregulation of the service sector, or the aging of its population; recovery requires tax cuts, or a massive bank reform, or maybe cannot be achieved at all until the economy has painfully purged itself of excess capacity. Some or all of these propositions may be true; but it is hard to know unless we have some clear framework for understanding the current predicament.
Economists of a certain age - basically my age and up - do have a theoretical framework of sorts for analyzing the situation: Japan is in the dreaded "liquidity trap", in which monetary policy becomes ineffective because you can't push interest rates below zero. The celebrated paper by Hicks (1937) that introduced the IS-LM model also showed, in the context of that model, how monetary policy might become ineffective under depression conditions. And for a long time macroeconomists kept the liquidity trap in mind as an important theoretical possibility, if not something one was likely to encounter in practice. But the IS-LM model, while it continues to be the workhorse of practical policy analysis in macroeconomics, has increasingly been treated by the profession as a sort of embarrassing relative, not fit to be seen in polite intellectual company. After all, even aside from the dependence of IS-LM analysis on the ad hoc assumption of price inflexibility, that analysis is at best a very rough attempt to squeeze fundamentally intertemporal issues like saving and investment into a static framework (a point which, incidentally, Hicks noted right at the beginning). As a result, IS-LM has been hidden away in the back pages of macroeconomic textbooks, given as little space as possible; and curiosa like the liquidity trap have been all but forgotten.
But here we are with what surely looks a lot like a liquidity trap in the world's second-largest economy. How could that have happened? What does it say about policy? For in a way the criticisms of IS-LM are right: it is too ad hoc, too close to assuming its conclusions to give us the kind of guidance we want. Indeed, many economists probably have doubts about whether anything like a liquidity trap is actually possible in a model with better microfoundations.
The purpose of this paper is to show that the liquidity trap is a real issue - that in a model that dots its microeconomic i's and crosses its intertemporal t's something that is very much like the Hicksian liquidity trap can indeed arise. Moreover, the conditions under which that trap emerges correspond, in at least a rough way, to some features of the real Japanese economy. To preview the conclusions briefly: in a country with poor long-run growth prospects - for example, because of unfavorable demographic trends - the short-term real interest rate that would be needed to match saving and investment may well be negative; since nominal interest rates cannot be negative, the country therefore "needs" expected inflation. If prices were perfectly flexible, the economy would get the inflation it needs, regardless of monetary policy - if necessary by deflating now so that prices can rise in the future. But if current prices are not downwardly flexible, and the public expects price stability in the long run, the economy cannot get the expected inflation it needs; and in that situation the economy finds itself in a slump against which short-run monetary expansion, no matter how large, is ineffective.
If this stylized analysis bears any resemblance to the real problem facing
Japan, the policy implications are radical. Structural reforms that raise
the long-run growth rate (or relax non-price credit constraints) might
alleviate the problem; so might deficit-financed government spending. But
the simplest way out of the slump is to give the economy the inflationary
expectations it needs. This means that the central bank must make a credible
commitment to engage in what would in other contexts be regarded as irresponsible
monetary policy - that is, convince the private sector that it will not
reverse its current monetary expansion when prices begin to rise!
This paper is in six parts. It begins by describing an extremely stylized
full-employment model of money, interest, and prices, a simplified version
of Lucas (1982). The next section shows that while under normal circumstances
prices in this model are proportional to the money supply, even when prices
are perfectly flexible there is a maximum rate of deflation that
cannot be exceeded no matter what the central bank does. And this maximum
rate of deflation can be negative - that is, under certain well-defined
circumstances the economy needs inflation, and with flexible prices will
get it regardless of monetary policy.
The third part introduces short-run price inflexibility, and shows that when an economy "needs" inflation, temporary monetary expansion - defined as expansion that does not raise the long-run price level - is completely ineffectual at increasing output. It is in this sense that an economy can indeed suffer from a liquidity trap. The fourth part then argues that making the analysis a bit less stylized - introducing investment and international trade - does not alter the basic conclusions: neither investment nor even the possibility of exporting excess savings to other countries necessarily eliminate the possibility of a liquidity trap. The fifth section argues that despite the highly stylized nature of the analysis, it does shed considerable light on Japan's quandary. Finally, the last part considers policy implications, especially the apparent implication that Japan may need to adopt more inflationary policies than any responsible person is now willing to propose.
1. Output, money, interest, and prices
The purpose of this paper is to demonstrate possibilities and clarify thinking,
rather than to be realistic. So I will concentrate on the simplest possible
fully-consistent model that establishes relationships among the four main
macroeconomic aggregates: output, the money supply, the interest rate,
and the price level. In this model individuals are identical and live forever,
so that there are no realistic complications involving distribution within
or between generations; output is simply given (i.e., it is an endowment
economy - an assumption I will relax later); and the demand for money arises
purely from a "cash-in-advance" assumption: people are required
to pay cash for goods.
Individuals are assumed to maximize their expected utility over an infinite
horizon; while the particular form of the utility function is not important,
for convenience I make it logarithmic, so that individuals maximize
U = ln(c1) + D ln(c2) + D2 ln(c3)
+ ...
where ct is consumption in period t, and D<1
is a discount factor. In each period individuals receive an endowment yt.
While I will think of this as a one-good economy, individuals cannot simply
consume their own endowment: they must buy their consumption from someone
else.
The purchase of goods requires cash. At the beginning of each period there
is a capital market, at which individuals can trade cash for one-period
bonds, with a nominal interest rate it. Their consumption
during the period is then constrained by the cash with which they emerge
from this trading: the nominal value of consumption, Pt ct
, cannot exceed money holdings Mt. After the capital
market is held, each individual purchases his desired consumption, while
receiving cash from the sale of his own endowment. There may also be a
transfer - positive or negative (a lump-sum tax) - from the government.
Finally, money is created or destroyed by the government via open market operations each period - that is, the government enters into the capital market and buys or sells bonds. The government also makes transfers or collects taxes (no government consumption at this point), and must obey its own intertemporal budget constraint, which takes into account any seignorage that may result from increases in the money supply over time.
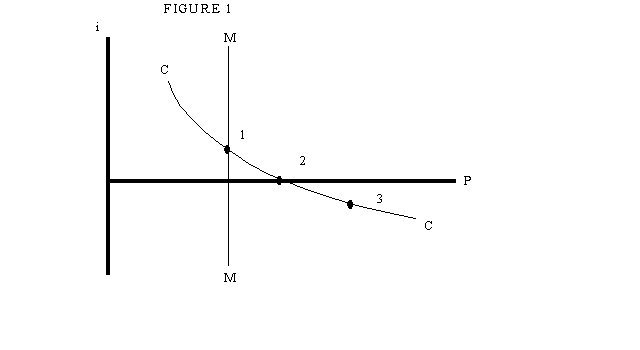
Analyzing this model in general requires a careful specification of the budget constraints of both individuals and the government, and of intertemporal choices. However, if we make some simplifying assumptions the model's implications can be derived with almost no algebra. Let us assume that from the second period onwards output (and therefore also consumption) will remain constant at a level y*, and that the government will also hold the money supply constant at a level M*. Then we can immediately guess at the solution from period 2 on: the price level will remain constant at P* = M*/y*, and the interest rate will also be constant at a rate i* = (1-D)/D. It is straightforward to confirm that this is indeed an equilibrium: one plus the real interest rate equals the ratio of marginal utility in any two successive periods; because the nominal interest rate is positive individuals have an incentive to acquire only as much cash as they need, so all money will indeed be spent on consumption.
All the action, then, goes into determining the price level and interest rate in the first period. Let us use un-subscripted letters to represent first-period output, consumption, interest rate, etc..
Our first relationship comes from the monetary side. Under normal circumstances - that is, when the nominal interest rate is positive - individuals will hold no more cash than they need to make their consumption purchases. So the cash-in-advance constraint will be binding:
Pc =Py = M, so that P = M/y
So under normal circumstances there is a simple proportional relationship between the money supply and the price level.
The second relationship comes from intertemporal choice. By holding one less yen in period 1, an individual gives up 1/P units of first-period consumption but allows himself to consume (1+i)/P* additional units in period 2. At an optimum this change must leave him indifferent. But the marginal utility of consumption in period 1, given the assumed utility function, is 1/c; the marginal utility in 2 is D/c*. It follows that we must have
c/c* = D-1 (P*/P)/ (1+i)
or
1+i = D-1 (c*/c) (P*/P)
or, finally, since consumption must equal output in each period,
1+i = D-1 (y*/y) (P*/P)
This says that the higher is the current price level, the lower the nominal interest rate. The easiest way to think about this is to say that there is an equilibrium real interest rate, D-1 (y*/y)-1 , which the economy will deliver whatever the behavior of nominal prices. Meanwhile, since the future price level P* is assumed held fixed, any rise in the current level creates expected deflation; hence higher P means lower i.
The two relationships are shown in Figure 1 as MM and CC respectively; as drawn, they intersect at point 1, simultaneously determining the interest rate and the price level. It is also immediately apparent that an increase in the first-period money supply will shift MM to the right, leading to a higher price level and a lower nominal (but not real) interest rate.
Figure 1
While this is surely the normal case, however, there is also another possibility,
to which we now turn.
2. When money becomes irrelevant
Suppose that you start with an economy in the equilibrium described by point 1 in Figure 1, and then imagine an initial open-market operation that increases the first-period money supply. (Throughout we imagine that the money supply from period 2 onwards remains unchanged - or equivalently that the central bank will do whatever is necessary to keep the post-2 price level stable). Initially, as we have already seen, this operation will increase the price level and reduce the interest rate. And such a monetary expansion can clearly drive the economy down the CC curve as far as point 2 in Figure 1. But what happens if the money supply is increased still further - so that the intersection of MM and CC is at a point like 3, with a negative nominal interest rate?
The answer is clearly that the interest rate cannot go negative, because then money would dominate bonds as an asset. What must therefore happen is that any increase in the money supply beyond the level that would push the interest rate to zero is simply substituted for zero-interest bonds in individual portfolios (with the bonds being purchased by the central bank in its open-market operation!), with no further effect on either the price level or the interest rate. Because spending is no longer constrained by money, the MM curve becomes irrelevant; the economy stays at point 2, no matter how large the money supply may be.
It is probably worth emphasizing here that the interest rate at point 2 is zero only on one-period bonds; it would not be zero on longer-term bonds, such as consols. This is important if one is trying to map the model onto the current situation in Japan, or for that matter the United States during the 1930s: long rates in Japan are positive, but short-term rates are indeed very close to zero.
A good way to think about what happens when money becomes irrelevant here is to bear in mind that we are holding the long-run money supply fixed at M*, and therefore also the long-run price level at P*. So when the central bank increases the current money supply, it is lowering the expected rate of money growth M*/M, and also - if it does succeed in raising the price level - the expected rate of inflation P*/P. Now what we know is that in this full employment model the economy will have the same real interest rate whatever the central bank does. Since the nominal interest rate cannot become negative, however, the economy has a minimum rate of inflation or maximum rate of deflation.
Now suppose that the central bank in effect tries to impose a rate of deflation that exceeds this minimum - which it does by making the current money supply M large relative to the future supply M*. What will happen is that the economy will simply cease to be cash-constrained, and any excess money will have no effect: the rate of deflation will be the maximum consistent with a zero nominal rate, and no more.
Now this may seem a silly thought experiment. Why would a central bank try to impose massive deflation? But the maximum rate of deflation need not be large, or even positive! Suppose that the required real rate of interest is negative; then the economy "needs" inflation, and an attempt by the central bank to achieve price stability will lead to a zero nominal interest rate, and excess cash holdings.
The condition under which the required real interest rate is negative is straightforward in this simple endowment economy. Market-clearing will require a negative real interest rate if the marginal utility of consumption in period 2 is greater than that of consumption in period 1, which will be the case if the economy's future output is expected to be sufficiently less than its current output. Specifically, given the assumed utility function, the required real interest rate is negative if
y/y* > 1/D
This condition may seem peculiar. After all, we normally think of economies as growing rather than shrinking! However, I will argue later that there are some real-world conditions under which the idea of declining endowment does not seem all that unreasonable - and that these conditions are fulfilled in Japan.
Of course, in a flexible-price economy even the necessity of a negative real interest rate does not cause unemployment. This conclusion may surprise those few readers who recall the tortured historical debate about the liquidity trap, much of which focussed on the question of whether wage and price flexibility were effective as a way of restoring full employment. In this model the problem does not arise - but the reason is a bit peculiar. What happens is that the economy deflates now in order to provide inflation later. That is, if the current money supply is so large compared with the future supply that the nominal rate is zero, but the real rate needs to be negative, P falls below P*; the public then expects the price level to rise, and this provides the necessary negative real interest rate. And to repeat, this fall in the price occurs regardless of the current money supply, because any excess money will simply be hoarded without adding to spending.
At this point we have something that is sort of like a liquidity trap: money becomes irrelevant at the margin. But aside from frustrating the central bank - which may have a thing about price stability, but finds itself presiding over inflation no matter what it does - this trap has no adverse real consequences. To turn this analysis into a real problem, in both senses, we need to introduce some kind of nominal rigidity.
3. The liquidity trap
Suppose, now, that the consumption good is produced rather than simply appearing, with a maximum productive capacity yf in period 1. And suppose, also, that this productive capacity need not be fully employed. In particular, I will simply assume that the price level in period 1 is predetermined - so that the economy now acquires a Keynesian feel, and monetary policy can affect output. (In period 2 and subsequently output will still be assumed to take on the value y*).
In this sticky-price world the level of period-1 consumption and output must still be equal, but now output adjusts to consumption rather than the other way around. Given the utility function, and the assumption that consumption will be y* in period 2, we can immediately write an expression for current real consumption, which becomes the "IS curve" determining real output:
c = y = D-1 y* (P*/P) (1+i)-1
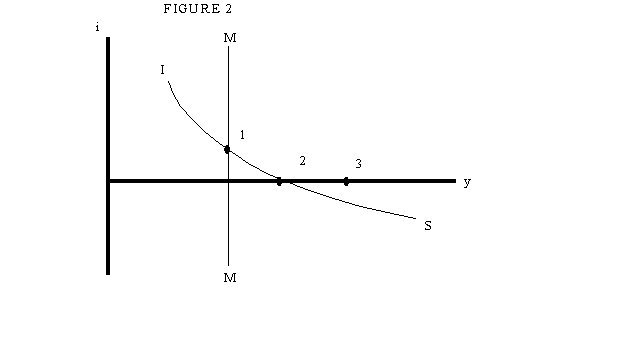
Figure 2 illustrates the joint determination of the interest rate and
output in this case. The curve IS, as just indicated, shows how output
will be determined by consumption demand, which is decreasing in the interest
rate. Meanwhile, as long as the nominal interest rate is positive, the
cash-in-advance constraint will be binding, so we will have the MM
curve
y = M/P
Figure 2
Increasing the money supply can now increase output, up to a point - specifically,
up to point 2. But what if productive capacity is at a point like 3? Then
the same argument as in the previous section applies: since the nominal
interest rate cannot go negative, any increase in money beyond the level
that drives the rate to zero will simply be substituted for bonds, with
no effect on spending. And therefore no open-market operation, no matter
how large, can get the economy to full employment. In short, the economy
is in a classic liquidity trap.
Under what conditions will a liquidity trap occur? One possibility is that P is high compared with P* - that people expect deflation, so that even a zero nominal rate is a high real rate. The other possibility, however, is that even if prices are expected to be stable, yf is high compared with the future - or to put it differently, peoples' expected future real income is low compared with the amount of consumption needed to use today's capacity. In that case, to persuade people to spend enough now may require a negative real interest rate, and with downwardly inflexible prices that may not be possible.
Or to put it yet another way, one that is closer to the language of applied macroeconomics: if people have low expectations about their future incomes, then even with a zero interest rate they may want to save more than the economy can absorb. (In this case, of course, the economy cannot absorb any savings - but I will come to that point below). And in that case, no matter what the central bank does with the current money supply, it cannot reflate the economy sufficiently to restore full employment.
So we have now seen that a fully specified model, which does not fudge either the role of money or the necessity of making intertemporal choices, can indeed generate a liquidity trap.
4. Investment at home and abroad
A liquidity trap can happen in a very simple economy - one in which there is no investment, and therefore no way for consumers in the aggregate to make tradeoffs between present and future. But can it still happen once we allow some way to use current production to buy future consumption - either by investing at home or acquiring assets abroad?
At first sight it might seem that allowing for investment and/or foreign trade should make nonsense of the idea that an economy needs a negative real interest rate to generate adequate demand. After all, even with diminishing returns the marginal product of capital is surely always positive; and one can always run a trade surplus, using the proceeds to buy foreign assets with a positive real return. Does this eliminate the liquidity trap as an interesting possibility?
To build a fully specified model with investment would require a longer and more elaborate paper. However, it is fairly straightforward to see that if we have a "Tobin's q" model of investment, in which periods of high investment are associated with a high real price of assets, a positive marginal product of capital is no guarantee that individuals face a positive real rate of return. To see why, suppose that for whatever reason consumers right now want to save a large fraction of their income. In order to persuade firms to invest that much, q must be high. But in the future, when consumers want to save less, q will be lower. Now while an investor who buys capital now will collect any rents on the capital - which will be positive as long as the marginal product of capital is positive - he must also take into account the prospective real capital loss as q declines from its current high level to a more normal level. As a result, to get the level of investment needed to absorb temporarily very high savings might require that investors be prepared to accept a negative real rate of return, and hence that the real interest rate be negative.
A basically similar argument applies to attempts to export savings, by investing abroad. If there are nontraded goods, export of capital will normally be associated with a depreciation in the real exchange rate, that is, a decline in the domestic price level compared with the foreign even when measured in a common currency. So if a country needs to export a lot of capital now, to be repatriated later, it will from its own point of view be buying foreign assets high, selling them low. Even though the real return in terms of foreign goods is certainly positive, the real return in terms of domestic consumption could well be negative.
Both of these points may be somewhat clearer if we try to think roughly of what they might mean in Japan's case. Suppose that we postulate that even at a zero real interest rate Japanese consumers insist on saving a great deal right now, but will probably save much less at some future date. To induce domestic firms to invest all those savings now would require a very high price of capital in place - say, a very high P/E ratio on Japanese stocks. But even a zero real interest rate might not be enough to get that P/E ratio, because stock prices would be limited by the expectation of an eventual fall. Similarly, to generate a trade surplus large enough to export all the savings would require a very weak real yen. Yet even a zero real interest rate (compared with positive rates abroad) might not generate sufficient depreciation, because the prospect of eventual appreciation would support the currency now.
So allowing for investment at home and abroad, while it may make a liquidity trap somewhat less plausible, does not make it impossible.
5. Is Japan in a liquidity trap?
Up to this point, I have tried to demonstrate that the idea of a liquidity trap, although originally arising in the context of a pseudo-static model, can be given a dynamically consistent interpretation. But just because something is possible does not mean that it is relevant. Do we really think that Japan is in a liquidity trap - and if it is, how did it get there?
An economy is in a liquidity trap if aggregate demand consistently falls short of productive capacity despite essentially zero short-term nominal interest rates. Japan certainly more or less meets the interest-rate criterion: at the time of writing the overnight money-market rate was 0.37 percent. The economy also certainly seems to be operating well below capacity. True, the OECD and IMF estimates of output gap are surprisingly modest, given the economy's lack of real growth since 1991. However, those numbers are based not on economic analysis but on a smoothing procedure that automatically builds any sustained slump into the estimated trend in potential output (using the same procedure on the United States in the 1930s finds the economy at full capacity by 1935). If one uses even a conservative estimate of Japanese potential growth since 1990 - say, 2 percent - the economy now appears to be in a very deep slump indeed.
If Japan is in a liquidity trap, however, why?
In the model of sections 1-3, a liquidity trap will arise only if future productive capacity is actually lower than current capacity. Before loosening that constraint, we can ask why one might expect Japan's future capacity to be relatively low compared with today's. And the obvious answer is demography: Japan's combination of declining birth rate and lack of immigration apparently means a shrinking rather than growing labor force over the next several decades. In the absence of productivity growth, potential output, say, 15 or 20 years out - y* in the model - could actually be below current capacity. Moreover, the labor force will drop faster than the population, because of shifting composition, so it is substantially easier to make the case that per capita productive capacity might actually be lower at some future date than it is today.
The case that a negative real interest rate is necessary can be strengthened if we allow for heterogeneity among individuals plus imperfect capital markets. Suppose that at any given time some people expect their future income to be higher than their current income, others expect it to be lower. In a perfect capital market those who expect their income to rise would tend to engage in dissaving. But suppose that this is difficult - that consumption loans are hard to come by. Then those who expect their income to rise will not contribute as much to the demand for funds as those who expect it to fall contribute to the supply, and the equilibrium real interest rate will be lower than it would have been in a more efficient capital market. Notice that we need not argue that Japanese capital markets are especially inefficient: this can be viewed simply as a reason why aggregate capacity need not actually be falling to require a negative real interest rate. But it is also true that at least some Japanese institutional pecularities - the relatively small use of credit cards, the high downpayments required on expensive houses (see Ito 1992) may contribute to the problem.
Moving outside the formal model, the prospects for a liquidity trap also depend on investment demand. Here demography again comes into play: the prospective decline in the labor force reduces the expected return on investments. And institutional problems, such as the troubles of the banking system, may also lead to some credit rationing that deters investment. And to the extent that firms are financially constrained by the debt run up in the past, they may be unable to invest as much as they otherwise would.
On the whole, while it is quite easy to make the case that Japan really is in a liquidity trap, it is much harder to give a convincing explanation of why. Demography seems to be the leading candidate; other "structural" reasons that are widely cited, while they do amount to an impressive litany of sins, do not necessarily explain why demand should be inadequate, as opposed to simply causing garden-variety microeconomic inefficiency. This lack of a clear link between the structural issues and the proximate problem has some important policy implications, as we will soon see.
6. What is to be done?
Japan is an economy that is almost certainly producing well below its productive
capacity - that is, the immediate problem facing Japan is one of demand,
not supply. And it gives every appearance of being in a liquidity trap
- that is, conventional monetary policy appears to have been pushed to
its limits, yet the economy remains depressed. What can be done? There
seem to be three main answers: structural reform, fiscal expansion, and
unconventional monetary policy. Let us consider each in turn.
Structural reform: Everyone agrees that Japan needs structural reform: it needs to clean up its banks, deregulate its service sector, reform its corporate accounting, and so on. But while such measures will increase the economy's microeconomic efficiency, will they help it recover? Bear in mind the trap shown in Figure 2: policy moves that increase yf, that is, which push point 3 to the right, do the economy no good if it is stuck at point 2 in any case. Measures that raise Japan's supply capacity but leave demand where it is will not help the situation; indeed, if unemployment rises as a result of increased efficiency the country might actually be worse off.
To be helpful in the current situation, structural reform must somehow induce people to spend more. It is possible to imagine several ways in which this might happen. A reformed financial sector might be able to lend to people and firms that are now credit-constrained. Deregulation might create new investment opportunities, raising investment demand. And conceivably reform might raise expectations of future income, encouraging higher spending now.
The striking thing about discussion of structural reform, however, is that when one poses the question "How will this increase demand?" - as opposed to supply - the answers are actually quite vague. I at least am far from sure that the kinds of structural reform being urged on Japan will increase demand at all, and see no reason to believe that even radical reform would be enough to jolt the economy out of its current trap.
Fiscal policy: The classic Keynesian view of the liquidity trap is, of course, that it demonstrates that under some circumstances monetary policy is impotent, and that in such cases fiscal pump-priming is the only answer. The framework here is rather different in its implications for monetary policy, but it does suggest that fiscal expansion could work. Obviously the model is subject to Ricardian equivalence, so that tax cuts would have no effect. But government purchases of goods and services in the first period, while they would be partly offset by a reduction in private consumption expenditures, could indeed increase demand and output.
While this policy could work, however, is it the right one for Japan? Japan has already engaged in extensive public works spending in an unsuccessful attempt to stimulate its economy. Much of this spending has been notoriously unproductive: bridges more or less to nowhere, airports few people use, etc.. True, since the economy is demand- rather than supply-constrained even wasteful spending is better than none. But there is a government fiscal constraint, even if Japan has probably been too ready to use it as an excuse. And anyway, is it really true that it is impossible to use the economy's resources to produce things people actually want?
Monetary policy: It may seem strange to return to monetary policy as an option. After all, haven't we just seen that it is ineffective? But it is important to realize that the monetary thought experiments we have performed have a special characteristic: they all involve only temporary changes in the money supply.
This point needs enlarging upon. Because the traditional IS-LM framework is a static one, it cannot make any distinction between temporary and permanent policy changes. And partly as a result, it seems to indicate that a liquidity trap is something that can last indefinitely. But the framework here, rudimentary as it is, suggests a quite different view. In the flexible-price version of the model, even when money and bonds turn out to be perfect substitutes in period 1, money is still neutral - that is, an equiproportional increase in the money supply in all periods will still raise prices in the same proportion. So what would a permanent increase in the money supply do in the case where prices are predetermined in period 1? Even if the economy is in a liquidity trap in the sense that the nominal interest rate is stuck at zero, the monetary expansion would raise the expected future price level P*, and hence reduce the real interest rate. A permanent as opposed to temporary monetary expansion would, in other words, be effective - because it would cause expectations of inflation.
Let us now bring this discussion back to earth, and to Japan in particular. Of course the Bank of Japan does not announce whether its changes in the monetary base are permanent or temporary. But we may argue that private actors view its actions as temporary, because they believe that the central bank is committed to price stability as a long-run goal. And that is why monetary policy is ineffective! Japan has been unable to get its economy moving precisely because the market regards the central bank as being responsible, and expects it to rein in the money supply if the price level starts to rise.
The way to make monetary policy effective, then, is for the central bank to credibly promise to be irresponsible - to make a persuasive case that it will permit inflation to occur, thereby producing the negative real interest rates the economy needs.
This sounds funny as well as perverse. Bear in mind, however, that the basic premise - that even a zero nominal interest rate is not enough to produce sufficient aggregate demand - is not hypothetical: it is a simple fact about Japan right now. Unless one can make a convincing case that structural reform or fiscal expansion will provide the necessary demand, the only way to expand the economy is to reduce the real interest rate; and the only way to do that is to create expectations of inflation.
Of course, it is not necessary that Japan do anything. In the quasi-static IS-LM version of the liquidity trap, it appears as if the slump could go on forever. A dynamic analysis makes it clear that it is a temporary phenomenon - in the model it only lasts one period, although the length of a "period" is unclear (it could be three years, or it could be 20). Even without any policy action, price adjustment or spontaneous structural change will eventually solve the problem. In the long run Japan will work its way out of the trap, whatever the policy response. But on the other hand, in the long run ...
REFERENCES
Hicks, J.R. (1937), "Mr. Keynes and the classics", Econometrica.
Ito, Takatoshi (1992), The Japanese Economy, Cambridge: MIT Press.
Lucas, R. (1982), "Interest rates and asset prices in a two-currency world", Journal of Monetary Economics 22, 3-42.