Paul Krugman
Nov. 1996
BUT FOR, AS IF, AND SO WHAT:
THOUGHT EXPERIMENTS ON TRADE AND FACTOR PRICES
In the last few years the impact of international trade on advanced-country wages has been hotly debated. Unusually, serious economists have not by and large argued about theory: with few exceptions they have agreed that a more or less classical Heckscher-Ohlin-Samuelson model is the best framework to use. Nor have they argued very much about the evidence. Instead, the major disputes have been philosophical: what does it mean to say that technology or trade has Acaused@ a given change in factor prices?
In this note I attempt to clarify and explain my own position in this debate. My view is that the most natural interpretation of an assertion that, say, international trade has Acaused@ wages for unskilled workers in advanced countries to decline by 2 percent is to view it as a Abut-for@ statement: but for the opportunities to import labor-intensive products offered by greater world integration, those wages would be 2 percent higher than they actually are. This interpretation leads, in turn, to the conclusion that the volume of trade must play a crucial role in any attempt to assess the effects of that trade; and it also leads to the conclusion that it is useful to calculate the factor content of trade - the net trade in factor services embodied in trade in goods.
To justify these claims, I present a sequence of three thought experiments on a simple trade model. There is nothing profound or difficult about these experiments - in fact, no algebra is necessary. The point, however, is that making sense of this debate is mainly a matter of asking the right questions; once you do so, the answers follow easily.
1. But for: International trade and domestic goods prices
There have been a number of papers, mainly by labor economists, in which regressions are run with labor market variables on the left-hand side and trade volumes - imports, exports, or balances - on the right hand side. Trade economists have been justifiably caustic about such analyses. After all, trade volumes are endogenous - they are driven at least as much by changes in a country=s own factor supplies, technology, and so on as they are by external forces. To run a regression of wages on import volume and then claim the coefficient as an estimate of the impact of trade on factor prices is a nonsensical exercise.
Some trade economists have, however, fallen into an almost equally severe fallacy by supposing that the answer is to put prices rather than quantities on the right hand side. The central issue in the trade-and-wages debate is the impact of North-South trade in manufactures on wages in advanced countries - that is, we are asking how trade with newly industrializing economies affects factor prices in the OECD. Given this, does it make sense to view world prices as exogenous? Surely not: since the OECD nations still account for most of gross world product, changes in their collective factor supplies or technology are as likely to affect trade prices as trade volumes.
If neither prices nor quantities are causal, however, what does it mean to say that trade caused or didn=t cause a change in factor prices? The answer, as pointed out by Deardorff and Hakura (1994), is to pose the question in Abut for@ terms. Specifically: in 1970 the newly industrializing countries had barely registered in international trade. Now they are a significant factor. How different would wages in advanced countries be if they were not - that is, how different would factor prices be but for the opportunities offered by the rise of the NIEs?
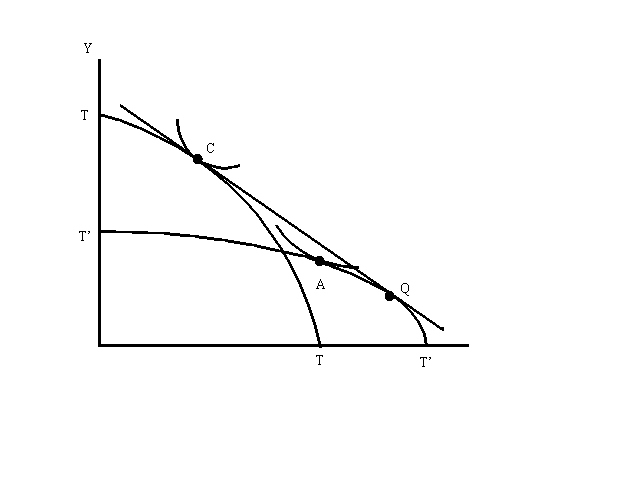
Figure 1 illustrates the basic argument. It represents the production, consumption, and trade of a stylized OECD. This stylized economy has two factors, skilled and unskilled labor, which it uses to produce skill-intensive X and labor-intensive Y. We suppose that the actual relative price of X is represented by the slope of the line PP, so that the OECD produces at Q and consumes at C., with CQ its trade vector with the rest of the world, assumed to consist solely of newly industrializing economies. (The curve passing through C and Q is the offer curve of the NIEs; it is shown to emphasize that this figure represents an equilibrium in which trade volumes and prices are, indeed, jointly determined).
Now pose the but-for question. How different would matters be if the opportunity to trade with the NIEs were not there? The answer, of course, is that the OECD would become autarkic (with respect to the NIEs - trade among OECD countries would continue), and goods prices within the OECD would have to change accordingly. At the no-trade equilibrium A, the relative price of X has fallen to the level indicated by the slope of the line P=P=. This fall in the relative price of the skill-intensive good would then, through the usual Stolper-Samuelson effect, raise the real wage of unskilled labor.
This thought experiment therefore suggests one procedure for estimating the effect of North-South trade on factor prices in advanced countries. First, construct a computable general equilibrium model of the OECD (notice that it is not necessary to model the NIEs), calibrated to reproduce the actual level of trade. Then determine the change in goods prices that would be necessary to induce the model OECD not to trade, to choose autarky. Finally, use the model again to determine the change in factor prices implied by that change in goods prices. This is exactly the procedure followed in Krugman (1995). Although that estimate was performed with a toy CGE model, the principle can be extended to any level of detail and sophistication one likes.
Some trade economists seem to find this straightforward thought experiment difficult to accept. The problem may be that they have learned too well from the critiques of naive trade-on-wages regressions that you can=t treat trade volume as exogenous. And doesn=t this approach depend crucially on the volume of trade? The appropriate answer, however, is so what? We are not trying to explain the time series behavior of factor prices in terms of the time series behavior of trade volumes. Instead, we are posing a static question: how large a change in relative goods prices (and hence factor prices) would be needed to eliminate the trade volume we currently see.
It is possible to stop at this point - to conduct the analysis in terms of goods prices and then derive factor prices indirectly. Such estimates suggest a significant but limited effect of trade on wages. The procedure, however, inevitably depends on highly debatable estimates of elasticities of substitution in both consumption and production. There is no way around these uncertainties. However, if we can Ascale@ the effect of trade on factor prices in some way - by showing, for example, that it is surely considerably smaller than the effects of changes in OECD factor supplies - then we may have greater confidence that at least the order of magnitude of our estimates is right. This is why it is helpful to show that the Abut-for@ approach to the impact of trade and wages also implies that it is appropriate to think of trade as an implicit kind of factor mobility, with the effect of trade on factor prices determined by the net trade in embodied factor services.
To do this, we need to do two more thought experiments, one on the effect of changes in factor supplies, then a final one showing the equivalence between such changes and the effects of trade.
2. Doing the two-step: Factor supplies and factor prices
For the next thought experiment, we consider not a trading economy but a closed one, and ask how changes in factor supplies change factor prices.
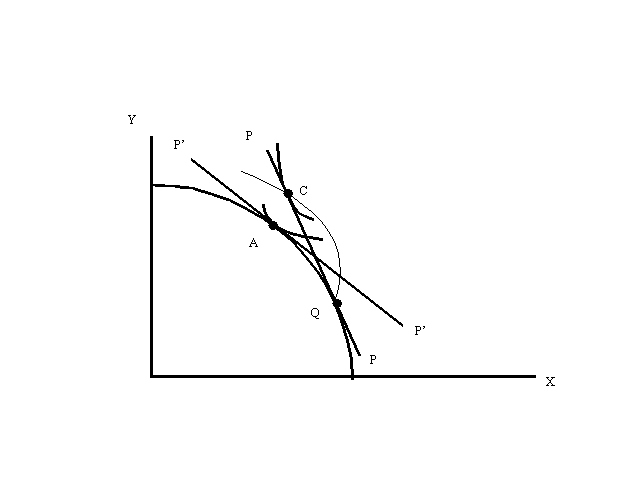
In Figure 2 , the transformation curve TT represents the initial production possibilities of the economy; its consumption and production are at point C.
We now imagine altering the factor endowment by adding skilled labor and subtracting unskilled labor. Let us suppose in particular that the changes in factor supplies are such that the total income of the economy measured at initial factor prices remains unchanged - i.e., that the market value of the unskilled labor subtracted equals the market value of the skilled labor added. This also implies that the total income of the economy will remain unchanged if goods prices remain the same. So the new production possibilities must look like T=T=, just tangent to the old budget line at a point like Q.
The initial goods and factor prices are, however, no longer consistent with equilibrium. At the original prices the economy would produce at Q, but it would still consume at C: there would be an excess supply of X and an excess demand for Y. To clear markets, the relative price of X would have to fall, leading to a new equilibrium at a point such as A. And of course factor prices would also change accordingly.
There is no necessary reason why we must think of the effects of a change in factor supplies in this two-step fashion. However, this thought experiment shows that the adjustment of a closed economy to an income-preserving change in endowment can be thought of as a two-step process: at unchanged prices output slides southeast along the original budget line, then prices change to put consumption on the new PPF. The usefulness of this way of thinking will become apparent in a moment.
3. As if: The factor content of trade
Let us now return to the situation described in part 1, where a stylized OECD engages in trade with newly industrializing countries. At this point we note that if we ignore the Aoriginal@ production possibility curve TT in Figure 2 and the NIE offer curve in Figure 1, the two diagrams are in fact identical.
This suggests that we can think of answering the Abut-for@ question about trade and factor prices in a somewhat different way.
We start with an economy producing at Q and consuming at C. We then imagine subtracting skilled labor from and adding unskilled labor to this economy in such a way as to leave its income at initial prices unchanged. If the hypothetical change in factor endowments is equal to the factor content of the real economy=s trade, we will end up with an economy whose production possibility curve is TT - that is, an economy whose autarky prices are the same as the prices at which the original economy trades. Let us call this the Aas-if@ economy, short for AAutarky with the Same Income and Factor prices@.
The punchline should now be obvious. The Abut-for@ change in goods and factor prices of part 1 - the difference between actual prices and those that would prevail but for the possibility of trade - is exactly the same as the change in prices that would occur if the factor content of actual trade were added back to the autarkic Aas-if@ economy. (Users of the factor content approach usually think of the thought experiment as being one of subtracting factors from the real economy rather than adding them back to a hypothetical autarkic economy. This alternative way of stating things may seem roundabout. However, by making it clear that the hypothetical economy is autarkic we also make it clear that goods prices are endogenous in the exercise).
In particular, we can now clarify the appropriate use for an often-maligned procedure. In a two-factor model, the log difference in relative factor prices due to trade may be estimated as the log difference in the ratio of factor supplies in the actual and Aas if@ economies, divided by the aggregate elasticity of substitution between these factors in the Aas if@ economy.
Is this reinterpretation - for that is all that it is - helpful? Why not simply stay with the approach in part 1? We can offer two answers.
First, even a 2-by-2 CGE model requires specifying three elasticities of substitution, one for each industry and one for consumption. This may make it seem as if estimating the effect of trade on factor prices depends in some complex way on these parameters, so that it would be hard to do any systematic sensitivity analysis. The factor content approach makes it clear, however, that all of these elasticities matter only insofar as they affect the aggregate elasticity of substitution between factors, and thus that sensitivity analysis can be undertaken simply by considering the plausible range of values for that aggregate elasticity.
Second, because the but-for experiment turns out to be equivalent to a change in the factor endowment of a hypothetical economy, it is meaningful to compare the scale of recent trade-induced changes in Aeffective@ factor supplies with actual changes in real factor supplies. What we find is that because the volume of North-South trade is small, the implicit exports of skilled and imports of unskilled labor by OECD countries are swamped by the increase in the actual skilled-to-unskilled ratio. This at least suggests that it is unlikely that trade has played a dominant role.
4. Not so fast? Objections
Judging from the recent denunciation of factor content calculations by Leamer (1996), there seem to be three main objections to their use.
First is the observation that trade volumes are endogenous. Yes, and so are trade prices. Since the nature of the but-for calculation has been repeatedly explained, it is unclear why this is still regarded as a valid objection.
Second, Leamer and others assert that the factor content approach is only valid if all production functions and tastes are Cobb-Douglas. As often stated, this objection seems to be based on a misunderstanding of what Deardorff and Staiger (1988) were saying. Certainly in a two-factor model the Cobb-Douglas assumption plays no role; and the case for using a two-factor model in this analysis is no worse than it is in any other context. Even in a multi-factor model, the basic proposition of factor content analysis remains completely valid. That is, the Abut-for@ consequences of a given level of trade are the same as those of adding the factor content of that trade to the Aas-if@ economy defined above.
What is true is that in a non-Cobb-Douglas world one cannot safely assume that the relative price of any two factors depends only on the ratio of their two endowments; in general it will depend on other factor supplies as well. This is really a point about the limits of Atwoness@ in trade modeling, not about factor content per se. And surely it remains true that if you change factor endowments, and the vector of changes is small (by whatever metric) relative to the initial vector, you would not expect large changes in factor prices, Cobb-Douglas or not. It therefore follows that if the volume of net trade in factor services is small, so must be the effects on factor prices.
Finally, the objection has been raised that the factor content approach is invalid in the face of trade imbalances. The same might be said of all CGE trade exercises: because the underlying model does not allow for trade imbalances, it is necessary either to introduce them by some ad hoc procedure or to represent the world by an approximate version in which trade is balanced. For most current purposes the latter approach seems adequate.
In the end, of course, one must return to the data. If one accepts that the factor content approach makes sense, one can then proceed to the problem of getting better estimates of the relevant numbers. These include factor contents themselves and, even more crucially, the aggregate elasticity of substitution.
REFERENCES
Alan Deardorff and Delia Hakura (1994), ATrade and wages - what are the questions?@ in J. Bhagwati and M. Kosters, eds., Trade and Wages: Leveling Wages Down? Washington: American Enterprise Institute, 1994.
Alan Deardorff and Robert Staiger (1988), AAn interpretation of the factor content of trade@, Journal of International Economics 24:93-107.
Paul Krugman (1995), AGrowing world trade: causes and consequences@, Brookings Papers on Economic Activity 1:1995.
Edward Leamer (1996), AWhat=s the use of factor contents?@, NBER Working Paper #5448.