DIMACS minimum cost flow problems

DIMACS (Center for Discrete Mathematics and Theoretical Computer Science (see http://dimacs.rutgers.edu/)) has formulated some 'challenges' for some specific problem instances (see http://dimacs.rutgers.edu/Challenges/). One of these challenges is network flows and matching - the first DIMACS implementation challenge.

One of these network flows are minimum cost flow problems:

Given a directed network with upper and lower capacities on each of its arcs, and given a set of external flows (positive or negative) that need to be routed through this network, find the minimal cost routing of the given flows through this network. Here, the cost per unit of flow on each arc is assumed to be known.

Network Structure

A network is a directed graph with n nodes and m arcs.
Nodes are identified by integers 1...n.
Graphs do not have to be symmetric: if an arc (v,w) is in the graph, the reverse arc (w,v) does not have to be in the graph.
Parallel arcs are not allowed.
Self-loops are not allowed.
Arc capacities are 32-bit signed integers.
The source and the sink are distinct.
The sink may be unreachable from the source.

There is a specific file format available for these kinds of problems:

The DIMACS minimum-cost flow format requires that bounds on feasible arc flows be integer-valued (the LOW and CAP fields described below). All files contain only ASCII characters with information collected on each line, as described below. A line is terminated with an end-of-line character. Fields in each line are separated by at least one blank space. Each line begins with a one-character designator to identify the line type.

The following information makes up a DIMACS minimum-cost flow input file:

comment lines
problem line
node descriptors
arc descriptors

As noted above, information is collected into lines, which begin with one-character designators. We describe each type of information line in turn.

Comment Lines: Comment lines give human-readable information about the file and are ignored by programs. Comment lines can appear anywhere in the file. Each comment line begins with a lower-case character c.
```
    c This is an example of a comment line.
```
Problem Line: There is one problem line per input file. The problem line must appear before any node or arc descriptor lines. For minimum-cost flow network instances the problem line has the following format:
```
    p min NODES ARCS
```
The lower-case character p signifies that this is a problem line. The three-character problem designator min identifies the file as containing specification information for a minimum-cost flow problem. The NODES field contains an integer value specifying n, the number of nodes in the network. The ARCS field contains an integer value specifying m, the number of arcs in the network.
Node Descriptors: All node descriptor lines must appear before all arc descriptor lines. For minimum-cost flow instances, the node descriptor lines describe supply and demand nodes, but not transshipment nodes. That is, only nodes with nonzero node supply values appear. There is one node descriptor line for each such node, with the following format.
```
    n ID FLOW
```
The lower-case character n signifies that this is a node descriptor line. The ID field gives a node identification number, an integer between 1 and n. The FLOW field gives the amount of supply at node ID.
Arc Descriptors: There is one arc descriptor line for each arc in the network. For a minimum-cost flow instance, arc descriptor lines are of the following form.
```
    a SRC DST LOW CAP COST
```
The lower-case character a signifies that this is an arc descriptor line. For a directed arc (v,w) the SRC field gives the identification number for the source vertex v, and the DST field gives the destination vertex w. Identification numbers are integers between 1 and n. The LOW field specifies the minimum abount of flow that can be sent along arc (v,w), and the CAP field gives the maximum amount of flow that can be sent along arc (v,w) in a feasible flow. The COST field contains the per-unit cost of flow sent along arc (v,w).

Input File Example :

The example network pictured here is followed by a corresponding DIMACS minimum-cost flow input file. Items listed in the lower-right of the graphic represent fields described above.

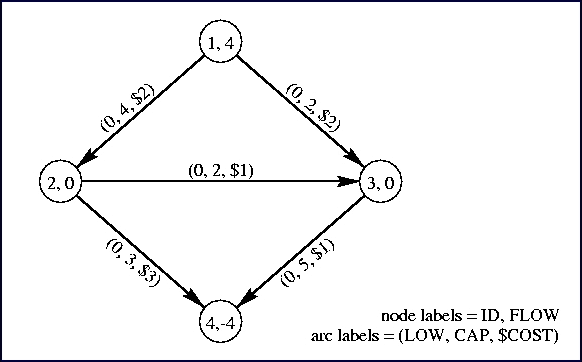
Minimum Cost Flow model graph

c This is a simple example file to demonstrate the DIMACS
c input file format for minimum cost flow problems. The solution
c vector is [2,2,2,0,4] with cost at 14.
c
c Problem line (nodes, links)
p min 4 5
c
c Node descriptor lines (supply+ or demand-)
n 1 4
n 4 -4
c
c Arc descriptor lines (from, to, minflow, maxflow, cost)
a 1 2 0 4 2
a 1 3 0 2 2
a 2 3 0 2 1
a 2 4 0 3 3
a 3 4 0 5 1
c
c End of file

lp_solve can read/write and solve these models via the xli_DIMACS XLI driver (see External Language Interfaces). It reads such a model in above format and solves it via linear programming. The xli can also generate a DIMACS formatted file.

For example:

lp_solve -rxli xli_DIMACS mincostflow.net

This gives as result:

Value of objective function: 14

Actual values of the variables:
C1                              2
C2                              2
C3                              2
C4                              0
C5                              4

Also from within the IDE, this XLI can be used. However, some entries must be added in LpSolveIDE.ini (in the folder where the IDE is installed).

In the [XLI] section the following must be added:

lib6=xli_DIMACS

And a new section for the DIMACS XLI must also be added:

[xli_DIMACS]
extension=.net
language=DIMACS

Then make sure that the xli_DIMACS.dll is available for the IDE. This must be done by placing this dll in the IDE folder or in the Windows system32 folder.

Solution :

The solution vector of above example is [2, 2, 2, 0, 4]
This must be interpreted as follows:
There are as many variables as there are arc descriptor lines in the input file and they appear in the same order. So:

C1 specifies how much flow there is for the first arc definition, in this case from 1 -> 2
C2 specifies how much flow there is for the second arc definition, in this case from 1 -> 3
C3 specifies how much flow there is for the third arc definition, in this case from 2 -> 3
C4 specifies how much flow there is for the fourth arc definition, in this case from 2 -> 4
C5 specifies how much flow there is for the fifth arc definition, in this case from 3 -> 4

This means there is a flow of 2 from node 1 to 2, a flow of 2 from node 1 to 3, a flow of 2 from node 2 to 3, a flow of 0 from node 2 to 4 and a flow of 4 from node 3 to 4.
The value of the objective is the cost of the flow: 2 * 2 + 2 * 2 + 2 * 1 + 0 * 3 + 4 * 1 = 14

Output :

The solution of the model can also be written in a DIMACS format:

comment lines
solution lines
flow assignments

For each network problem, the solution is an integer-valued flow assignment. The output file should list the solution and flow assignment for all arcs in the graph. As noted above, information is collected into lines, which begin with one-character designators. We describe each type of information line in turn.

Comment Lines: Comment lines give human-readable information about the file and are ignored by programs. Comment lines can appear anywhere in the file. Each comment line begins with a lower-case character c.
```
    c This is an example of a comment line.
```
Solution line. The solution line contains the flow value and has the following format:
```
    s VALUE
```
The lower-case character s signifies that this is a solution line. The VALUE field contains the value of the objective.
Flow assignments. There is one flow assignment line for each arc in the input network. These lines have the following format:
```
    f SRC DST FLOW
```
The lower-case character f signifies that this is a flow assignment line. For arc (u,v), the SRC and DST fields give v and w, respectively. The FLOW field gives the amount of flow assigned to arc (u,v).

lp_solve can generate a solution file via the xli_DIMACS XLI driver (see External Language Interfaces).

For example:

lp_solve -rxli xli_DIMACS mincostflow.net -wxlisol xli_DIMACS mincostflow.sol

This generates the following solution contents:

c mincostflow.net
c
c Dimacs-format minimum cost flow result file
c generated by lp_solve
c
c Solution
s 14
c
c SRC DST FLOW
f 1 2 2
f 1 3 2
f 2 3 2
f 2 4 0
f 3 4 4
c
c End of file

lp_solve can also generate a solution file with only non-zero values.

For example:

lp_solve -rxli xli_DIMACS mincostflow.net -wxlisol xli_DIMACS mincostflow.sol -wxlisolopt "-nz"

This generates the following solution contents:

c mincostflow.net
c
c Dimacs-format minimum cost flow result file
c generated by lp_solve
c
c Solution
s 14
c
c Only non-zero flows are written
c SRC DST FLOW
f 1 2 2
f 1 3 2
f 2 3 2
f 3 4 4
c
c End of file

A testset of models can be found at http://elib.zib.de/pub/Packages/mp-testdata/mincost/
Also see the dimacs ftp site: ftp://dimacs.rutgers.edu/pub/netflow