How to design a production line that has a bottleneck

Problem: suppose we are designing a 20-machine production line. The machines have been selected, and the only decision remaining is the amount of space to allocate for in-process inventory. The common operation time is one operation per minute. The target production rate is .88 parts per minute. The goal is to determine the smallest amount of in-process inventory space so that the line meets that target.

Three production lines have been optimized in the figure. That is, we have found the minimal total inventory space required to produce .88 parts per minute for three different lines. The figure displays how that space is distributed.

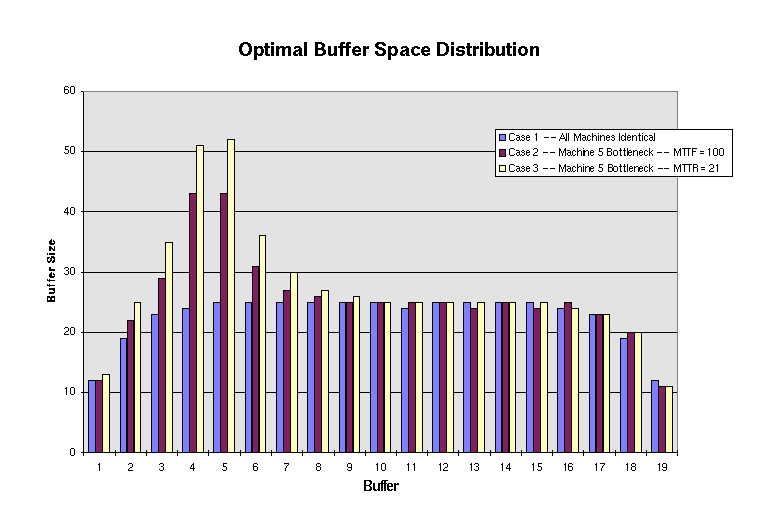
In Case 1, each machine is unreliable with mean time to fail (MTTF) 200 minutes and mean time to repair (MTTR) 10.5 minutes. Every machine could therefore operate in isolation at rate .95 parts per minute on the average, and easily meet the target. However, if there were no in-process inventory allowed, each machine's failure would cause every other machine to be forced idle, and the actual production rate would only be .487. To achieve the target production rate, the minimal required inventory space is room for 430 parts, distributed according to the figure.

Case 2 and 3 are similar to Case 1, except that Machine 5 (and only Machine 5) is replaced by a less reliable model. In both cases, the reliability of Machine 5 is reduced to .905. In Case 2, MTTF = 100 and MTTR = 10.5 minutes; In Case 3, MTTF = 200 and MTTR = 21 minutes. There is thus a well-defined bottleneck.

With no buffering between the machines, the production rate of both Cases 2 and 3 would be .475. Again, each machine (including the bottleneck) could meet the required production rate in isolation, but the complete system cannot without inventory buffering between the machines. The minimal required total inventory space is room for 485 parts for Case 2 and 523 for Case 3.

Summary

Line	Production rate with no buffers	Minimal buffer space for production rate target (.88 parts/min)
Case 1	.487	430
Case 2	.475	485
Case 3	.475	523

• The additional inventory space is allocated approximately symmetrically around the bottleneck, but it is not all placed precisely at the bottleneck.

• Case 3 needs more space than Case 2. This suggests that increased repair time is worse than increased failure frequency.

• Case 1 exhibits the inverted bowl phenomenon, observed by Hillier, So, and Boling (1993). A line with identical machines requires less buffer space at the ends because of the usual assumption that the first machine is never starved and the last machine is never blocked.

• Especially sharp-eyed readers may notice that the graphs look a little uneven. This is due mainly to the fact that we have restricted the solution to integers: we are assuming that the line is producing discrete items. In addition, the results shown may be slightly non-optimal.

The zero-buffer production rates were calculated from the work of Buzacott (1968). The optimal distributions of buffer space were calculated from Gershwin and Goldis (1995) and Schor (1995).

References:

J. A. Buzacott (1968), ``Prediction of the Efficiency of Production Systems without Internal Storage,'' Int. J. Prod. Res., Vol. 6, No. 3, pp. 173-188.

S. B. Gershwin and Y. Goldis (1995), ``Efficient Algorithms for Transfer Line Design,'' MIT Laboratory for Manufacturing and Productivity Report LMP-95-005, November, 1995, 50 pages.

F. S. Hillier, K. C. So, and R. W. Boling (1993), ``Toward Characterizing the Optimal Allocation of Storage Space in Production Line Systems with Variable Processing Times,'' Management Science, Volume 39, Number 1, January, 1993, pp. 126-133.

James E. Schor (1995), ``Efficient Algorithms for Buffer Allocation,'' M.S. Thesis, MIT EECS; MIT Laboratory for Manufacturing and Productivity Report LMP-95-006, May, 1995.

Copyright © Massachusetts Institute of Technology 1996. All rights reserved.