How to Use the Membrane Theory to Analyze Masonry Domes Graphically

This tutorial explains how to use the online applet to analyze a masonry dome based on the method of William S. Wolfe as described in Graphical Analysis: A textbook on graphic statics (Wolfe 1921). Wolfe's method treats the dome as a membrane with zero thickness whose line of thrust, or force line, follows the median radius of the dome.  For a more detailed background on this graphical analysis method, see the Methodology page.

Overview

This java applet was developed using Cabri Geometry II software by Texas Instruments.  To learn more about Cabri, visit www.cabri.com.

Two key rules for using this applet follow:

1) "Ctrl" key + mouse drag will shift the viewing window.

2) In general, bright blue open-circle points are parameters that the user can control.

   This tutorial is divided into four parts as shown:

    I. User-Defined Parameters

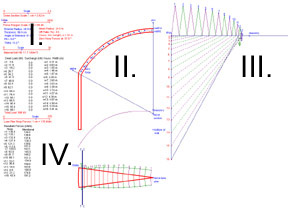
    II. Representative Dome Section

    III. Force Polygon

    IV. Representative Lune in Plan.

I.  User-Defined Parameters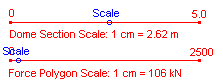

1. Four sliding scales are located on the left of the screen.  Use these scales to define the structure's geometry and the user interface.  The minimum and maximum of these values are shown and may not be modified.

   1. Dome Section Scale: Adjusts the appearance of the representative dome section in terms of 1 cm on the screen = n meters actual structure.
   2. Force Polygon Scale: Adjusts the force polygon in terms of of 1 cm on the screen = n kiloNewton's (kN) force.
   3. Material Unit Weight: Requires user input to specify the unit weight (kN/m³) of the basic material of the masonry.  This will be treated as a uniform load.  Uniform live and snow loads and concentrated loads, etc., are considered as surcharge weight in this applet, and should not be included as Material Unit Weight.
   4. Lune Plan Hoop Forces: Adjusts the appearance of the hoop resultant forces on the plan view of the individual dome lune.

2. Five geometric parameters in blue text located below the first two sliders require user definition.

   1. Exterior Radius: Move the point "radExt." on the centerline of the representative dome section up or down to specify the exterior radius of the dome.  Note that the scales may require additional adjustment.
      
   2. Thickness: Move the point "radInt" on the centerline of the dome section.  This applet assumes if the interior radius is known, then the thickness is known, and vice versa.  Note that thickness is in units of centimeters.
      
   3. Angle of Embrace: Move the point "alpha" on the dome section to modify the angle of embrace.  The angle of embrace is the amount of a sphere that the dome encompasses, and is measured from the crown of the dome to its base.
      
   4. Oculus Angle: Move the point "phi" on the dome section to modify the opening.  The oculus angle is the angle of the opening at the crown of the dome measured from the crown.  A dome with no oculus will have a zero phi value.
      
   5. Theta: Move the point "Theta" on the lune plan view to modify this value.  Theta represents the number of lunes into which the dome is approximated in plan view.  The maximum theta is 15 degrees, which is equivalent to dividing the dome into 24 wedges.  Larger theta values reduce the accuracy of this analysis method.

3. The applet automatically calculates the following parameters using the dome's geometry: the mean radius, thickness-to-radius (t/R) ratio, and the arc length of one voussoir (u).

   1. Dead Load (kN): The dead load of the masonry is determined by the dome's geometry.
      
   2. Total Load (kN):  The total load represents the total load of the uniform and surcharge loads for the individual lune.  To find the total weight of the dome, multiply this value by (360/theta).
      
   3. Zero hoop forces at --- is determined by the zero hoop point described below.

II.  Representative Dome Section

1. The dome section is evenly divided into 16 voussoirs:

   1.    The u value represents the arc length of one voussoir along the mean radius and is constant for all voussoirs.

   2.    The w values represents the mean width of each voussoir in plan, and increases from crown to base.

    

2. The median radius is shown in alternating purple and green segments.

3. To include surcharge on specified regions of the dome, move the bright blue points, some labeled with numbers, at the center of gravity of the appropriate voussoir.  Note that this analysis assumes axis-symmetrical loading.  Surcharge located at one location on this representative lune will be assumed to occur in a ring around the dome.

4. Zero hoop point: Move the point "zero hoop" to the intersection of the masonry vector and median radius.  This will determine the angle at where zero hoop forces occur.

5. Masonry point: Move the point "masonry" along the centerline until the masonry vector intersects the median radius at the number determined by the force polygon.

6. Move section: Move the point "move section" to shift the dome section around the screen.

7. Bottom of wall: Move the blue point "bottom of wall" to elongate the wall section, which acts only to enhance the perspective of the dome section.

III.  Force Polygon

1. The force polygon is a graphical representation of the internal and external forces of the structure.  Details on interpreting the force polygon are included in the Methodology section.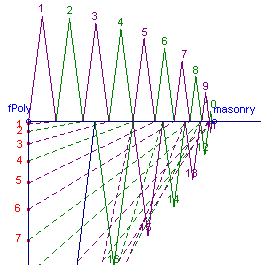

2. The vertical line with the red numbered points represent the loads on the dome for each voussoir.

3. The diagonal segments intersecting the vertical line at the red points and the horizontal ray of the force polygon represent the internal meridional forces.

4. The triangular polygons along the horizontal ray numbered in pink and green values represent the internal hoop forces.

5. fPoly: Move the point "fPoly" to move the force polygon around the viewing screen.

6. Masonry: If the dome to be analyzed is masonry, that is, the structure has little capacity to resist tensile forces, then slide the point "masonry" along the horizontal line until it intersects the location of outermost diagonal line (where the hoop force polygons transition from above to below the dark blue horizontal ray).

   1. Note the number of the last triangle hoop force polygon above the horizontal ray.

   2. On the representative dome section, slide the point "masonry" up the dome centerline until the pink masonry vector intersects the median dome radius at the center of gravity point with the same number from Step 1 above.

   3. This is the modified line of thrust for a masonry structure.  Note its deviation from the median radius.

   4. Move the "zero hoop" point along the median radius to this point of intersection.

IV. Representative Lune in Plan

1. The Average Resultant Forces (kN/m) are provided on the left hand side of the screen for each voussoir i.

   

   1.  Hoop values: to find the total hoop force of a voussoir, multiply this value by u, the arc length of one voussoir.

   1. Note that hoop forces are maximum compression at the crown of the dome, decrease to near zero, and then increase in tension.  This corresponds with the dip in the forces shown on the plan view of the lune from the center to perimeter.

   2. T | C divider: This vertical divider should be located approximately where the hoop forces become zero.  To the left of the divider, hoop forces are in tension.  For the case of masonry of masonry structures, hoop forces are zero to the left of this line.  To the right of the divider, hoop forces are in compression.

   2.  Meridional values: to find the total meridional force of a voussoir, multiply this value by w_i, the mean width of a voussoir.

   1. Meridional force resultants listed are the values occurring through the center of gravity of the voussoir.  From the force polygon, the meridional force resultant of voussoir i is given by the average length of meridional force segments which define the voussoir top and bottom edges, or (m_i + m_i-1) / 2.

   2. Meridional forces are always compressive and increase from the dome's crown to base.

2. Representative Lune in Plan

   

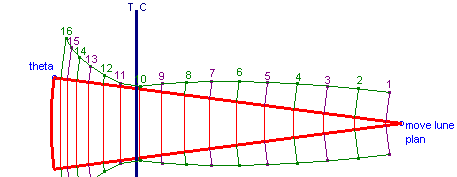
   1. Theta: Move point "theta" to define the number of individual lunes into which the dome is divided.

   2. Move lune plan:  Slide this point along the dome centerline to move the lune plan in the viewing window.

Return to applet.

Go to Methodology.

Return to Analysis of Masonry Domes HomePage.