ReaxFF modeling of fracture

ReaxFF Modeling of fracture of silicon: Integration of chemistry and mechanics

To appear in Phys. Rev. Lett., 2006 ("Multi-paradigm modeling of dynamical crack propagation in
silicon using the ReaxFF reactive force field" by Buehler, van Duin and Goddard).

Abstract: We report a study of dynamic cracking in a silicon single crystal in which the ReaxFF reactive force field is used for several thousand atoms near the crack tip while more than 100,000 atoms of the model system are described with a simple nonreactive forc field. The ReaxFF is completely derived from quantum mechanical calculations of simple silicon systems without any empirical parameters. Our results reproduce experimental observations of fracture in silicon including differences in crack dynamics for loading in the [110] or [100] orientations and dynamical instabilities with increasing crack velocity. We also observe formation of secondary microcracks ahead of the moving mother crack.

Atomistic modeling of materials in which formation and breaking of chemical bonds plays an important role in determining their mechanical behavior has so far been a quite difficult and in some cases an impossible endeavor. This is because most empirical interatomic potentials cannot describe breaking and for ma tion of bonds between various chemical elements correctly. Up to date, only quantum mechanical (QM) methods, for example those based on density functional theory (DFT) can be used. However, the number of atoms accessible to most QM methods is limited to about 100 atoms and to very short time scales.

An accurate treatment of bond breaking and for ma tion at scales relevant to mechanical properties of ma terials involves thousands of atoms, as for example at crack tips, dislocation cores, and grain boundaries or at other defects. Our new concept of reactive potentials (ReaxFF) can overcome some of the limitations imposed by DFT theories and enables large-scale simulations of thousands of reactive atoms with QM accuracy. ReaxFF, originally only developed for hydrocarbons has been extended recently to cover a wide range of ma terials, including metals, semiconductors and organic chemistry, which enables to describe thousands of reactive atoms in complex biological systems such as enzymes.

Figure 1: Simulation geometry. We use a hybrid approach in which the crack tip modeled by a reactive potential ReaxFF is embedded into a large nonreactive region (Tersoff).

Our approach provides an alternative to other multi-scale schemes that integrate QM(DFT, TB) with empirical potentials.

We focus on applying ReaxFF to model deformation and fracture of nanostructures of silicon and silicon oxides. Our computational results show good agreement with experimental observations, including crack instabilities, crack speeds and crystallographic dependence of fracture dynamics. We further demonstrate the competition of chemical processes, as for example oxidation, with brittle crack extension. Our new methods allow, for the first time, a thorough coupling of complex chemistry with larger length and time scales relevant for mechanical properties of materials.

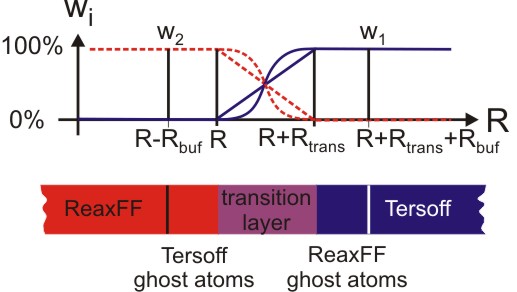
Figure 2 (top) : Handshaking of the reactive and nonreactive region.

Figure 3 (right): Our model allows modeling the correct crack dynamics, as shown here for a crack moving in the [110] crystal direction forming (110) crystal surfaces. Our results clearly show that unlike for the pure Tersoff model in which the crack doesn't propagate, in the hybrid multi-paradigm model the crack extends and the material behaves brittle.

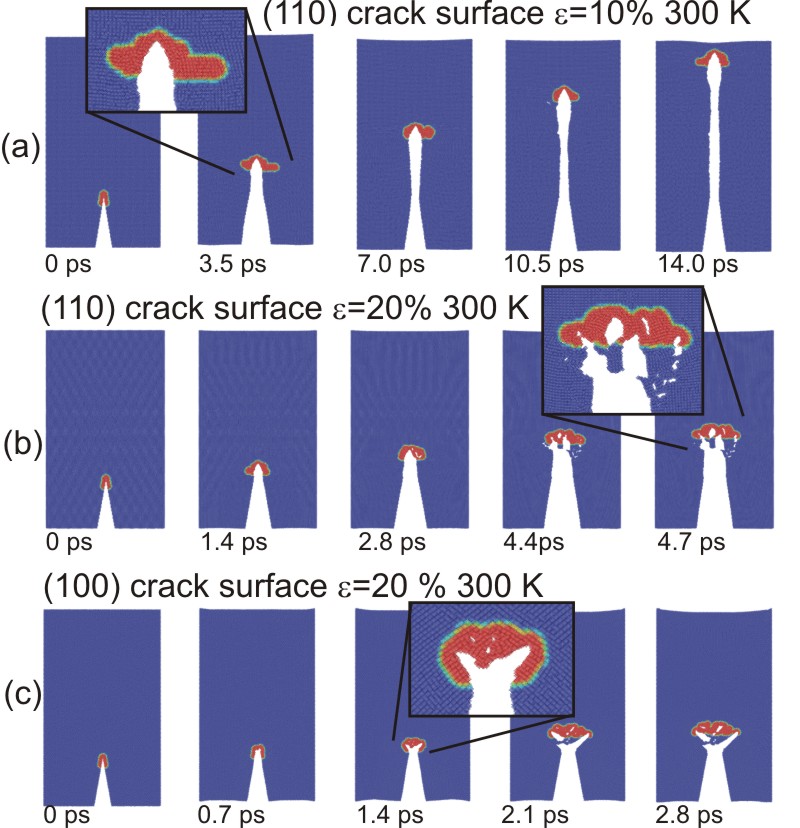
Figure 4 : Crack propagation in different crystallographic directions and under different applied load. As can be seen in subplot (b), we observe formation of microcracks ahead of the primary crack as the crack gains speed. It can also be observed that the crack becomes unstable and leads to formation of increasingly rough surfaces with higher crack speed. The instability generating rough, uneven crack surfaces sets in at a fraction of the Rayleigh-wave speed. Subplot (c) shows that a crack initially oriented in the [100] direction branches off into the [110] direction. This is in agreement with theory (lower fracture surface energy) and experiment.

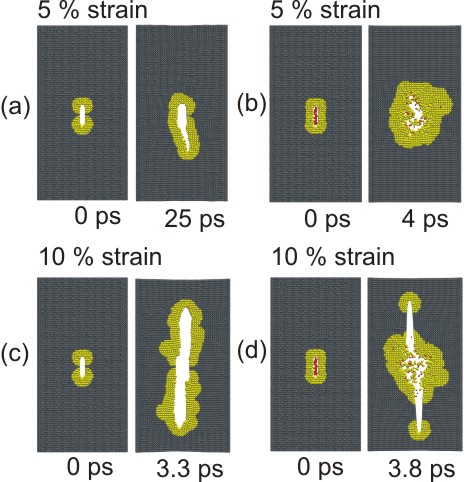
Figure 5: The true potential of our new method can be seen in this example, showing how reactive regions capable of treating oxygen-silicon interactions can be embedded in large nonreactive regions.