
refer+ing, the result
that you get is refering instead of referring.
The direct technical problem here is that whenever Kimmo attempts to add the
second "r", gemination15 fails. Essentially, the doubling of the
letter "r" is only permitted by gemination15 if it is in state 14.
However, without a symbol to indicate the stressed syllable in the word,
it won't ever do anything aside from staying in state 1 or rejecting.
Practically, we need to always provide the stress indicator for these
machines to work, and indeed generating from the string re`fer+ing
works properly, as shown in this screenshot:
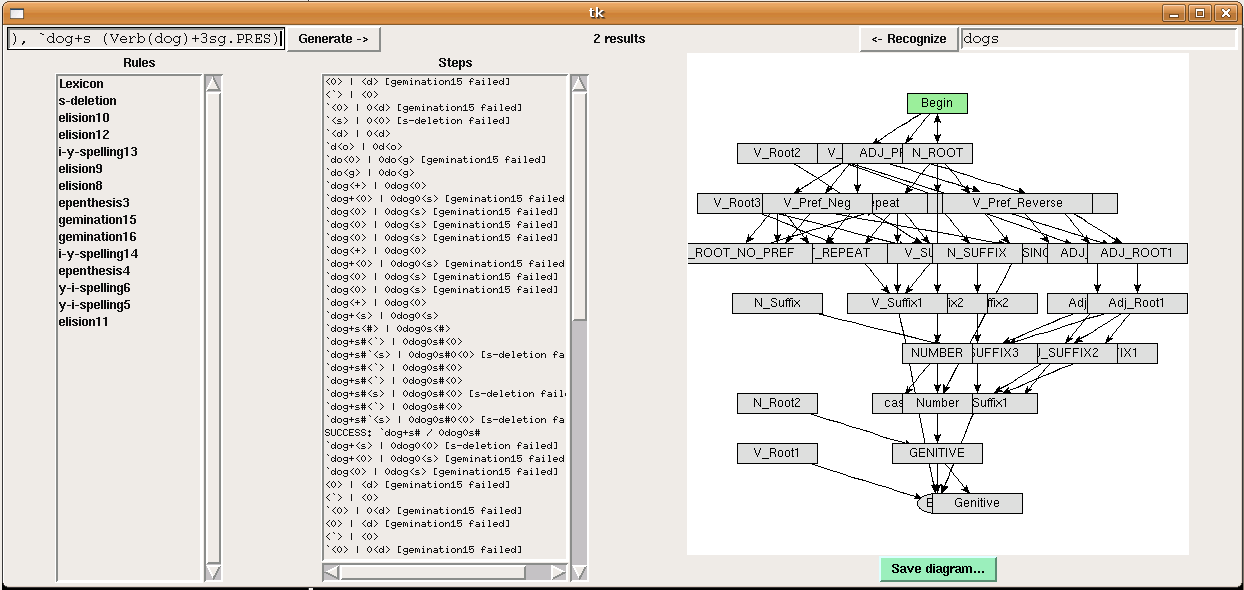
dogs is
`dog+s (Noun(dog)+PL). I added "dog" as a verb by putting
the following line in the V_ROOT_NO_PREF section of the
lexicon:`dog AfterVerb Verb(dog)
flier, it at first
appears that the system is making more than one left-to-right pass across
the word to find it. However, this is not strictly speaking the case.
It is making a single pass across the word, and backtracking as far as
necessary when it fails. In this case, it fails after it has gone through
most of the word and finds that it needs to backtrack pretty much all the
way to the beginning. That is, essentially Kimmo is running a depth-first
search. This means that while Lauri Kartunnen's quote claiming that "the
recognizer only makes a single left-to-right pass through the string as it
homes in on its target in the lexicon" is technically not wrong, there are
some cases in which it will appear to be misleading.
The actual issue that causes Kimmo's recognizer to have to backtrack all
the way in this case can be identified by stepping through the recognition
steps and watching the states that the lexicon is in. Up until the point
of backtracking, most of the states hint that it is trying to recognize
"flier" as a form of the noun "fly." Beyond the backtracking, most of
the lexicon states hint that it is trying to recognize "flier" as a form
of the verb "fly." Thus, we may expect to see this sort of behavior when
the root of a word may be used as multiple different parts of speech.
This behavior will not occur with generation because generation
only cares about spelling change rules, and since it doesn't care about
parts of speech at all, it makes no use of the lexicon. This is the key
way in which it differs from recognition.
Success, the machine does not actually
loop back at all. What is actually happening is just a continuation of
the depth-first search that it has been conducting all along. Misunderstanding
this is a result of failing to grasp the crucial point that the rules
should not be thought of as driving the process of generation to some end;
instead, the rules are filters, whose only purpose is to weed out
and reject the impermissible words. Kimmo needs to generate all
allowable words, and so it must eventually travel all the branches in its
depth-first search until each one either results in a complete valid
word, or is rejected by one or more of the filters (rules).
rule12.yaml appear in,
the output is kampat. The lab asks us to compare this with
what we hypothesized, and in fact this exactly matches what I expected to
happen, having read the Kimmo documentation that was suggested. However,
someone who had not yet familiarized themselves with the way Kimmo worked
would have expected the rules to be applied in the opposite order from
that order which they appeared to be applied in previously.
This is not the case because Kimmo does not order rules at all; all
the rules apply simultaneously, and can reference information in both
the underlying lexical representation and the surface form. They don't
feed one another; they each simply limit what the outputs from the total
system may be. There is, of course, another reason someone with the
above hypothesis would be confused... if rule 1 had been applied and
then rule 2 had been applied, the expected output would be kammat,
but it was actually kampat. Perhaps this is actually an
error in the way these rules are ordered in the lab.
Rather than take the rules as originally written in the lab, I felt
that the syntax used there was insufficiently expressive in that it doesn't
reflect the true two-level nature of the Kimmo engine. Specifically,
it doesn't specify whether the various elements of the environments are
constrained with respect to the lexical form, the surface realization, or
both. Thus, considering the generation we wished to happen, I rewrote the
rules in the much more expressive syntax outlined in the Kimmo documentation,
and proceeded to compile those into FST tables, discarding the original
implementations entirely. In essence, I think the problem was posed in
a strange way, and that suggesting that we modify the machines to interact
"better" is going about the problem the wrong way - properly written
two-level rules should not have to care much about one another, and if
the rules are expressed correctly at the outset, this problem shouldn't
exist in the first place.
The rules I implemented in my file, corresponding to the functions performed
by the original rules, are as follows:
# p:m <= @:m ___
p realized as m: |
FSA
p @ p @
m m @ @
1: 1 2 1 1
2. 1 1 0 1
# N:m <= ___ p:@
N realized as m: |
FSA
N N p @
m @ @ @
1: 1 2 1 1
2. 1 2 0 1
kammat from kaNpat
while rejecting kampat.
>>> k=load("rule12mine.yaml")
>>> print list(k.generate('kaNpat', TextTrace(3)))
p realized as m: 1 => 1
N realized as m: 1 => 1
k
k
p realized as m: 1 => 1
N realized as m: 1 => 1
ka
ka
p realized as m: 1 => 2
N realized as m: 1 => 1
kaN
kam
p realized as m: 2 => 1
N realized as m: 1 => 1
kaNp
kamm
p realized as m: 1 => 1
N realized as m: 1 => 1
kaNpa
kamma
p realized as m: 1 => 1
N realized as m: 1 => 1
kaNpat<#>
kammat<#>
p realized as m: 1 => 1
N realized as m: 1 => 1
kaNpat#
kammat#
SUCCESS: kaNpat# <=> kammat#
kaN
kam
p realized as m: 2 => 0
N realized as m: 1 => 1
['kammat']