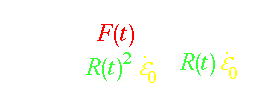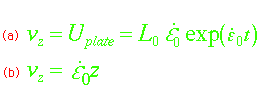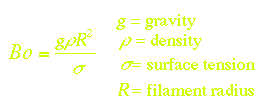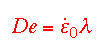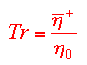Extensional Rheology Experiment (ERE)
This work is sponsored by NASA Grant NAG3-1385. The Extensional Rheology
Experiment (ERE) is part of NASA's microgravity flight program, in which an
experiment is flown in one of NASA's microgravity platforms.
For an up to date survey of filiment streching rheometry, please see the
International Congress on Rheology (2000)
proceeding.
 |
Justification for Microgravity
Gravitational body forces cause appreciable sagging of fluid filaments when
they are deformed in a uniaxial extensional flow. This sagging is most
notable for low deformation rates where strain-hardening is not significant.
Removing these forces will allow one to probe a wider parametric range of
strain rates, while simulataneously measuring the total stress exhibited by
the deforming fluid, the molecular level orientation of the polymer chains
in the fluid, and the velocity field of the fluid. |
First off, you need to understand what rheology means. In short,
rheology is the study of the fluid response of a material to an imposed stress.
Extensional rheology focuses on pulling on a piece of material in a purely
extensional manner, i.e. no shear. This is the type of flow you would see if you
stretched a rubber band. A shearing flow would be the response of the rubber
band if you laid it on a flat surface and slid your hand over it. The rubber
band extends slightly, then tumbles over and contracts, repeating this action
over and over again. In an extensional flow, the rubber band will continue to
elongate until you can not stretch it any further.
It is easy to see that the amount of force required to stretch the rubber
band is considerably greater than than required to shear the rubber band. The
stress, or the force/area, is higher in the extensional deformation due to
extent of the deformation. Entropic forces, which want to randomize the
configuration of the rubber band, resist the deformation, which aligns the
macromolecules that make up the rubber band. Whence, the stress increases as the
deformation increases.
How does this apply to polymer materials? A polymer material is
anything that contains long molecules composed of repeat units. Take a small
molecule, like ethane. Link several ethane units together, forming a chain. Keep
doing this until you have roughly 10,000-100,000 ethanes, or repeat units. This
is now a polymer molecule with the name polyethylene, the material from which
milk jugs are made.
 |
A polymer chain is like a string of spaghetti, which can wind around,
double over on itself, and become entangled with other polymer chains. The
more entangled the chains, the more difficult it is to deform them, in
either shear or in extension. This resistance to deformation rate is called
viscosity. The greater the resistance to deformation, the greater the
viscosity. |
Polymer melts,such as polystyrene (PS), polymethylmethacrylate (PMMA), and
polyethylene (PE), consist of highly entangled polymers that are heated to a
temperature where polymer chain motion is possible. Because these materials are
so entangled, the viscosity is very high, on the order of 106-108
times the viscosity of water.
Extensional rheology experiments conducted on polymer solutions were carried out
with a filament stretching rheometer designed and constructed in our laboratory.
The design is based on the concept first discussed by Cogswell (Plast. Polym.,
36, 109 (1968)) then later refined by Sridhar et al. (J.
Non-Newtonian Fluid Mech., 40, 217 (1991)). A small sample of fluid
is placed between two circular endplates. The top plate is moved, and we monitor
the total force on the bottom plate (F), and the minimum radius (R). For more
details on the experimental technique, please refer to our
method paper. The extensional viscosity
is computed from the expression
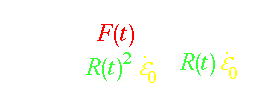
The second term represents the force contribution from the static surface
tension (sigma), which is subtracted so that we only monitor the stress arising
from viscous terms.
The top plate moves with the velocity profile described by (a) Lagrangian
Frame (i.e. moving with the fluid) (b) Eulerian Frame (i.e. fixed lab position)
|
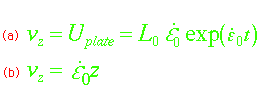
|
With this profile, the velocity gradient dv/dz is a constant for
all values of z (where z is the axial position along the
deforming filament. This constant is equal to the strain rate. In other
words, the strain rate will be uniform everywhere in the filament during the
entire deformation. Therefore, the stress will be uniform everywhere in the
filament, which simplifies the interpretation of the data. |
| The initial filament diameter is small, typically 3-7 mm in
diameter. This small value assures that surface tension will dominate the
initial gravitational body forces. The dominance of either term is often
represented as a Bond Number (Bo), a dimensionless term that
describes the ratio of gravitational forces to surface tension forces. For
these materials and sample dimensions, we typically get Bo < 0.1,
indicating the domination of surface tension over gravity. While this may be
accomplished with a small radius, we can also achieve the same effect by
reducing the effective density through the use of a surrounding
density-matched fluid, or by reducing gravity. |
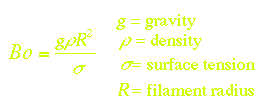 |
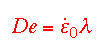 |
The response of the fluid to the imposed strain rate is a function of
the relative magnitude of the strain rate to the relaxation time of the
fluid. This relaxationship is called the Deborah number (De), which
is the ratio of the characteristic responsetime of a fluid to the
characteristic flow time. A large De means that the fluid cannot keep
up with the deformation rate. In other words, the material will look more
elastic that viscous, and responds more like a Hookian spring. Similarly,
De << 1 means that the fluid is essentially all viscous (i.e.
Newtonian). For 0.5 < De < 10, the fluid exhibits both viscous and
elastic behavior, and is thus a region of interest. |
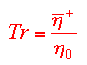 |
For the experiment shown below, the fluid relaxation time is 3.8
seconds, giving a Deborah Number De = 2.5. As a result, the material
should initially look like a Newtonian sample, then look more and more
elastic as the polymer chains begin to align and stretch out in the flow.
Termed "strain hardening," the extensional viscosity will begin to increase.
The extensional viscosity is often non-dimensionalized with the shear
viscosity. This ratio is called the Trouton Ratio . For a Newtonian
fluid, the Trouton ratio Tr=3. |
As the plot shows below, the non-Newtonian fluid initially reaches a Tr=3,
then increases by 3 orders of magnitude. After the deformation halts, the
polymer chains relax, cause the stress and hence the Trouton ratio to decrease.
Because the material has strain-hardened, the filament radius remains constant
for several seconds after cessation of stretching.